true
Redundant Paths
USACO 2006 January Gold
提高+ /省选-
#3498db
- Luogu P2860
- AcWing 395
- BZOJ #1718
题目要求我们给一个无向联通图上加几条边,使得整个图变成一个双联通分量。
我们可以想到的一个思路就是,首先跑一遍 Tarjan 算法,将所有的双连通分量缩成点,这样就可以将整张图缩成一棵树。
这样的话,我们可以瞎搞出来一个结论,如下:
我们统计出来所有的叶子结点,记其数目为 $cnt$,我们最终要加的边数最少就是 $\lceil \dfrac{cnt}{2} \rceil$。
首先我们可以随便连接两个叶子结点,将其变为一个基环树。
我们可以证明,一定有一种连接方法,使得得到的基环树是有偶数条支链的。
如果我们得到的基环树有奇数条支链的话,我们可以进行一些转化:
假设当前有这样一个基环树:
(不如叫他1-乙基-3-(1-甲基)乙基环己烷)
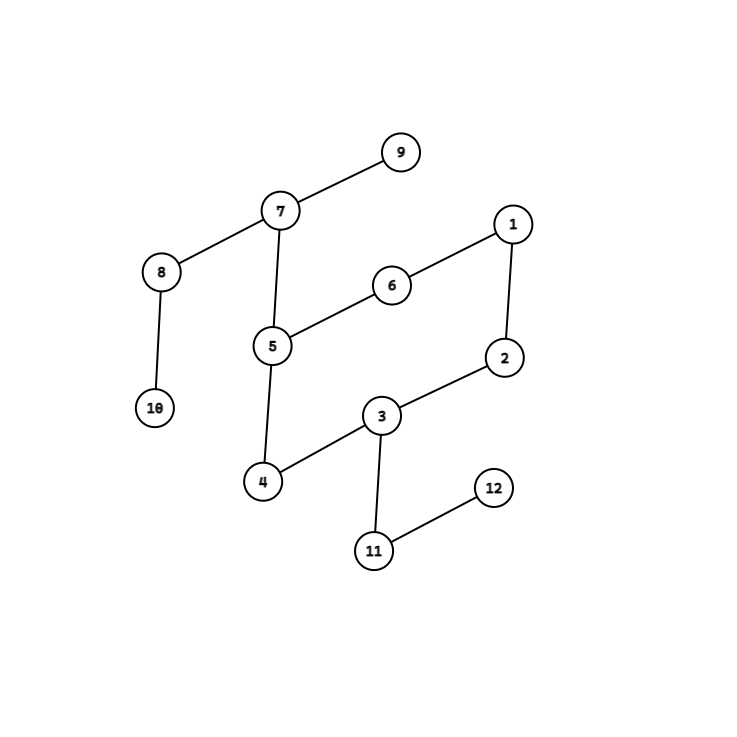
我们可以找到一条边,连接两个端点,而其中一个端点有支链。不妨设这个有支链的点为 $y$,另一个点为 $x$。
我们断开连接 $x$ 与 $y$ 的边,然后找到 $y$ 的一条支链最底端的叶子结点 $z$,最后连接 $x$ 与 $z$,减少了一条支链。
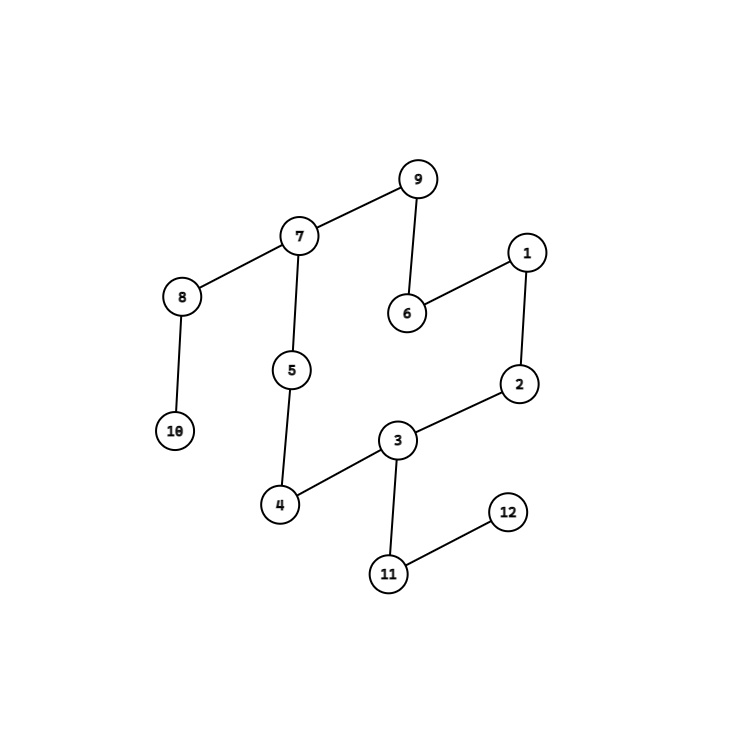
(不如叫他1,4-二乙基环辛烷)
这样就可以变成只有偶数条支链了。
对于每一条支链的叶子结点,我们找到一个另外的叶子结点,使得他们的LCA在环上。这样就满足了我们“双联通分量”的要求。不懂的可以自己手画一下。
但是有些时候随机连接的方案不一定能让所有的LCA都在环上,比如这个:
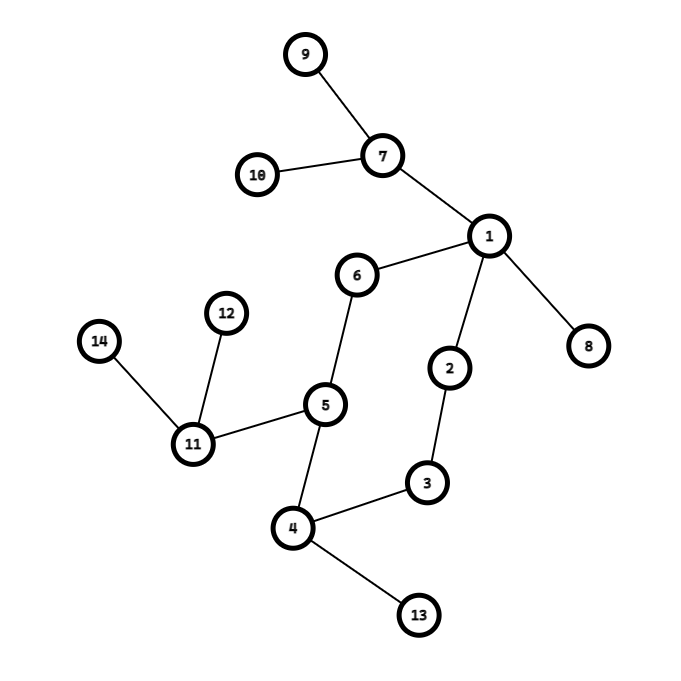
这样连接就不可以:
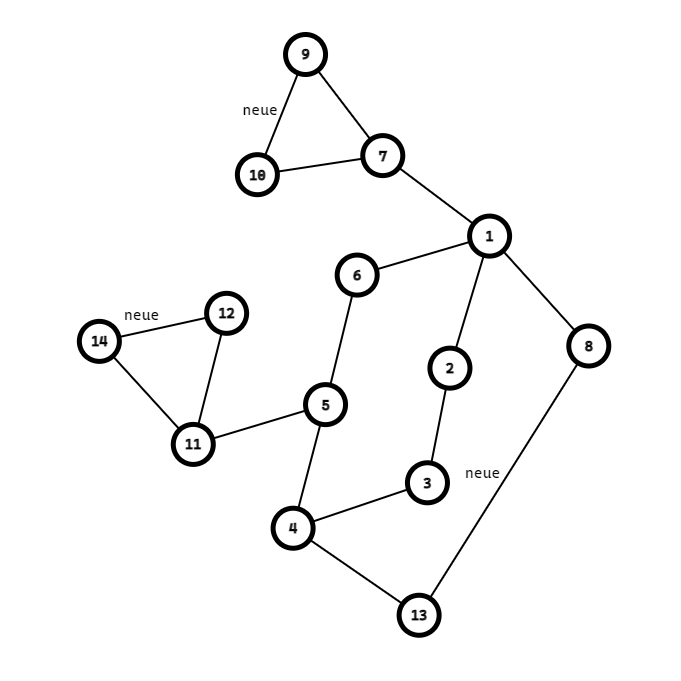
这样连接就可以:
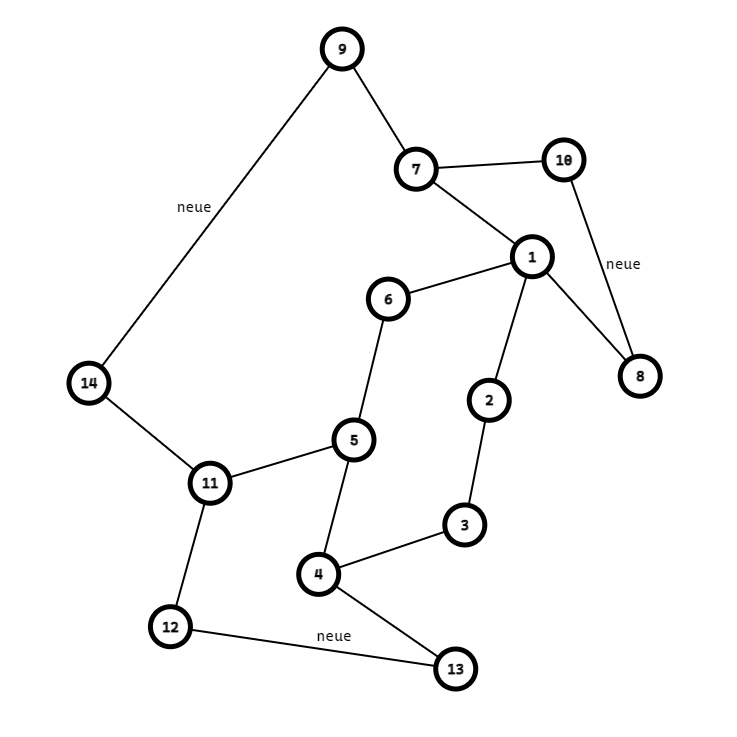
但是很不幸,上面的那种情况就是出现了。
现在我们考虑由其转移到一个可行的方案上面。
因为我们总共有偶数个叶子结点,所以我们最终还是会剩偶数个叶子结点没有配对。
我们可以通过不断对部分节点重新配对来缩小问题规模,直至解决问题。
我们先把不对劲的边断开:
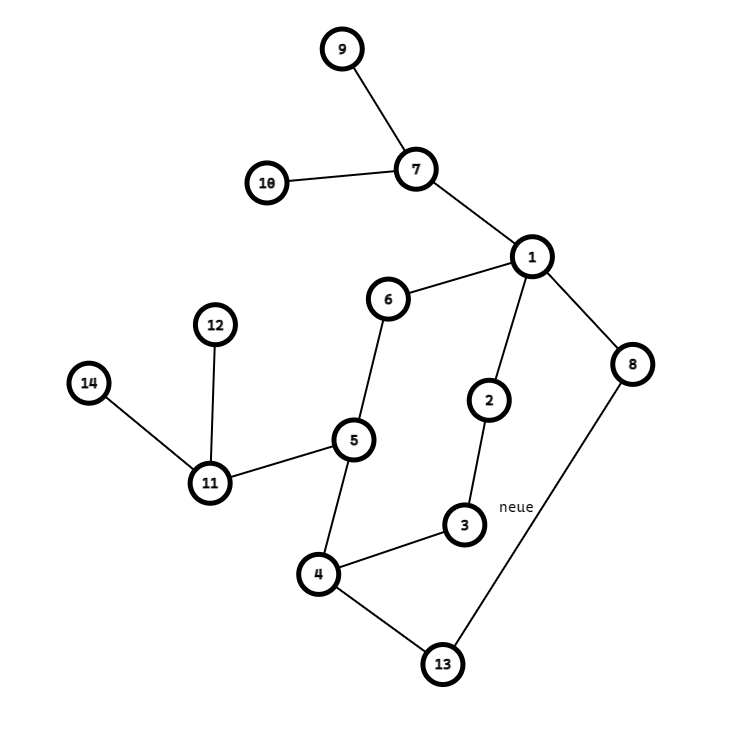
然后找到已经配好对了的两个子节点,这里选取8和13;
断掉其间的边,然后分别找一个子树上的任意一个点连边;
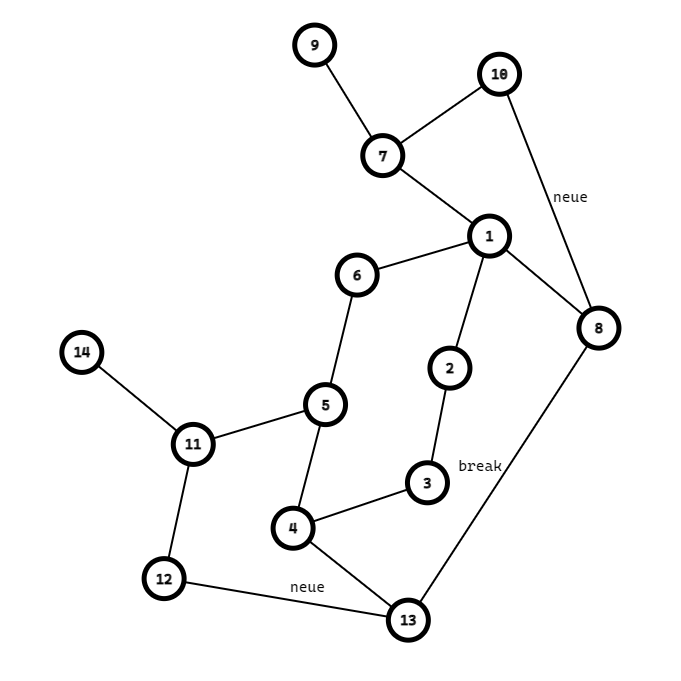
然后我们的问题规模就缩小了2,剩下的点如法炮制即可。
如果最终只剩两个点,而且不在同一支链上的话就直接连边即可。
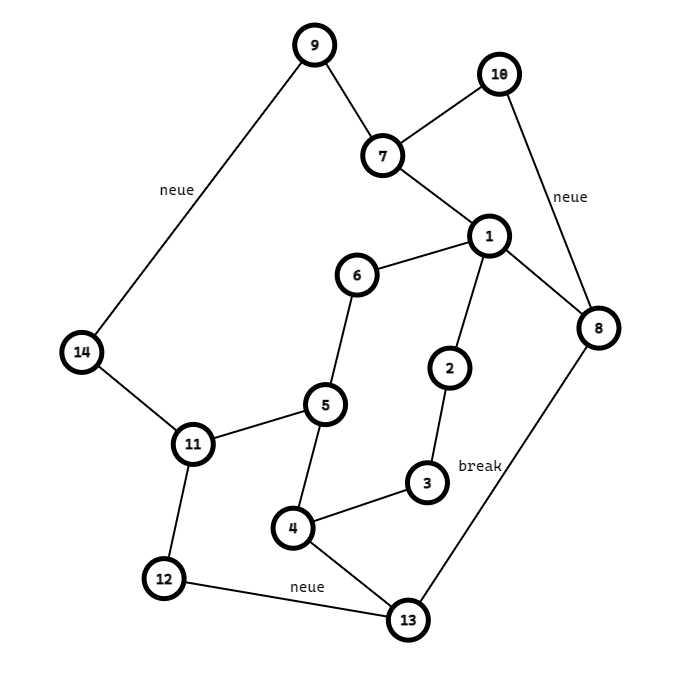
最终我们可以得出,我们最少需要连接的边数是 $\lceil \dfrac{cnt}{2} \rceil$ 条。
然后就可以上代码了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 10010, M = 200010;
int n, m;
int h[N], e[M], ne[M], idx;
int isBridge[M];
int dfn[N], low[N], cnt;
int sta[N], tt;
int scc[N], sc, sz[N];
int deg[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void tarjan(int p, int from)
{
low[p] = dfn[p] = ++cnt;
sta[++tt] = p;
for(int i = h[p]; ~i; i = ne[i])
{
int j = e[i];
if(!dfn[j])
{
tarjan(j, i);
low[p] = min(low[p], low[j]);
if(dfn[p] < low[j])
isBridge[i] = isBridge[i ^ 1] = true;
}
else if(i != (from ^ 1))
{
low[p] = min(low[p], dfn[j]);
}
}
if(dfn[p] == low[p])
{
++sc;
while(sta[tt] != p)
{
scc[sta[tt]] = sc;
sz[sc]++;
tt--;
}
scc[sta[tt]] = sc;
sz[sc]++;
tt--;
}
}
int main()
{
memset(h, -1, sizeof(h));
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++)
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
tarjan(1, -1);
for(int i = 0; i < idx; i++)
if(isBridge[i])
deg[scc[e[i]]]++;
int cnt = 0;
for(int i = 1; i <= sc; i++)
if(deg[i] == 1)cnt++;
printf("%d\n", (cnt + 1) / 2);
return 0;
}
|







