网络流 做题记录
网络流相关做题记录。
(我为什么要造孽放代码上来……)
目录
网络流24题
- LibreOJ #6000 / Luogu P2756 飞行员配对方案问题 >
- LibreOJ #6001 / Luogu P2762 太空飞行计划问题 >
- LibreOJ #6004 / Luogu P3254 圆桌问题 >
- LibreOJ #6007 / Luogu P2774 方格取数问题 >
- LibreOJ #6008 / Luogu P1251 餐巾计划问题 >
- LibreOJ #6011 / Luogu P4015 运输问题 >
- LibreOJ #6012 / Luogu P4014 分配问题 >
- LibreOJ #6013 / Luogu P4016 负载平衡问题 >
- LibreOJ #6015 / Luogu P2754 [CTSC1999] 家园 >
- LibreOJ #6122 / Luogu P2770 航空路线问题 >
- LibreOJ #6224 / Luogu P4012 深海机器人问题 >
最大流
- Luogu P1343 地震逃生 >
- Luogu P2472 [SCOI2007] 蜥蜴 >
- Luogu P2891 [USACO07OPEN] Dining G >
Luogu P1402 酒店之王 ^
Luogu P1231 教辅的组成 ^ - Luogu P3701 主主树 >
- LibreOJ #2239 / Luogu P3163 [CQOI2014]危桥 >
二分图
- Luogu P7368 [USACO05NOV] Asteroids G >
最小割
- Luogu P3931 SAC E#1 - 一道难题 Tree >
- Luogu P1345 [USACO5.4] 奶牛的电信Telecowmunication >
- Luogu P2057 [SHOI2007] 善意的投票 / [JLOI2010] 冠军调查 >
- Luogu P4177 [CEOI2008] order >
- Luogu P1361 小M的作物 >
费用流
- Luogu P1004 [NOIP2000 提高组] 方格取数 >
- Luogu P1006 [NOIP2008 提高组] 传纸条 >
- Luogu P2457 [SDOI2006] 仓库管理员的烦恼 >
- Luogu P2517 [HAOI2010] 订货 >
- Luogu P2153 [SDOI2009] 晨跑 >
上下界网络流
- Luogu P5258 [JSOI2013] 旅行时的困惑 >
网络流24题
飞行员配对方案问题
英国飞行员连向源点,外籍飞行员连向汇点,可以搭配的英国飞行员连向外籍飞行员。边权均为 $1$。
跑一遍最大流即可。
最后枚举所有边,如果当前边连接一个外籍飞行员和一个英国飞行员,且其容量为空,那么这条边就被流经过,说明这条边代表的一堆飞行员可以配对,输出两端点即可。
太空飞行计划问题
这是一个最大权闭合子图问题。我们可以将这个转化为一个最小割问题。
讲解可以见我博客的另外一篇文章。
其中,实验就是正权点,仪器就是负权点,建图连边即可。
圆桌问题
因为我们想要让坐在一个桌子旁的人两两不属于同一个代表团,那就可以转化为让一个代表团的人分散在不同的桌子上。
于是我们将所有的代表团和桌子都抽象成点。
我们从源点向每个代表团的点连一条容量为代表团人数的边,再从每一张桌子向汇点连一条容量为桌子容量的边。
然后我们将每一个代表团都向每一个桌子连一条容量为1的边。
最后跑最大流,得到的得数就是最多能给多少个人安排上桌子。
如果有人没有安排上桌子,那么久直接输出0即可。
如果所有人都安排上桌子了,就搜一下来确定方案。
方格取数问题
我们一旦取走一个数,那么这个数周围的四个格子里面的数就不能被取走了。
那我们可以转化一下,不考虑允许,而是考虑禁止。
那我们就可以按照权值和最小的原则来得到一种方案并取出,剩下的就是我们所要求的方案。
那我们按照国际象棋棋盘的染色方案进行染色,即对于位于第 $i$ 行 $j$ 列的点,如果 $i+j$ 为奇数则向源点连一条边权为当前格子权值的边,并同时向周围四个点连一条边权为无限大的边;否则连向汇点,边权为当前格子权值。
由于最小割最大流定理,我们在求出最大流之后,拿所有格子的权值总和减去最大流即使我们要的答案。
餐巾计划问题
我们这样连边:
- 源点与餐厅输出连一条容量为当天用量,费用为0的边;
- 汇点与餐厅输入连一条容量为当天用量,费用为0的边;
- 餐厅输出与下一日的餐厅输出连一条容量为无限,费用为0的边。
- 源点与餐厅输入连一条容量为无限,费用为 $p$ 的边;
- 餐厅输出与 $n$ 天后的餐厅输入连一条容量为无限,费用为 $s$ 的边,代表快洗部;
- 餐厅输出与 $m$ 天后的餐厅输入连一条容量为无限,费用为 $f$ 的边,代表慢洗部。
然后跑一个最小费用最大流即可,最终的费用就是答案。
运输问题
费用流。
源点向仓库连边,仓库向商店连边,商店向汇点连边。
跑费用流即可。
分配问题
费用流。
源点向工人连边,工人向工件连边,工件向汇点连边。
跑费用流即可。
和上一道题惊人地相似。
负载平衡问题
首先每个点向左右两边的点连边,费用为1,然后:
如果这个点多于平均值,那就向源点连其权值与平均值之差;
如果这个点少于平均值,那就像汇点连其权值与平均值之差。
这两种边的费用为0。
然后跑费用流即可。
[CTSC1999]家园
首先我们需要判断一下地球和月球是否联通,这个只需要使用并查集即可。
然后我们枚举天数,直到某一天转移的人达到要求了之后就停止循环,并输出天数。
我们在枚举的时候,逐天按照飞船的行进路线加边。因为每一次飞船都需要花一天时间来走一次的路程,所以我们每一条边都是从某一天的某一个站点到下一天的下一个站点,容量为飞船容量。
然后每一天跑最大流,得到的最大流结果就是当天以及之前所有天的转移人数总和。
航空路线问题
题目要求我们找到一条从起点城市到重点城市再回到起点城市的路径,并要求除起点城市外每一个点只能经过一次。
我们考虑拆点,除起点和终点容量为2之外容量均为1,然后按照飞机航线来建边,容量为1。
当然这样我们是不可能得出最大经过的城市个数的,我们需要用到费用流的手段。
我们将每个城市拆点的时候建的边的费用赋为1,其他的边赋为0。
然后我们跑费用流即可。
然后题目还让我们输出一个可能的方案。
于是我们就直接大暴搜就可以了。
还要注意起点终点直通的情况。
深海机器人问题
这个就是很明显的最大费用最大流,我们只需要把生物标本的价值抽象成为费用即可。
按照题目要求,我们每一个点都向上和向右分别建两条边,一条代表采集了生物标本,容量为1价值为c,另外一条代表已经被采集完了,容量为无限价值为0。
把所有的可以出发的坐标连向源点,容量为 $k$;所有的可以作为目的地的坐标连向汇点,容量为 $r$。
然后跑一遍费用流即可。
最大流
地震逃生
最大流板子,只不过在跑之前先要用并查集来判断一下连通性。
当然也可以直接跑,判断最大流量是否为0。
[SCOI2007] 蜥蜴
这道题在做之前得首先解决平面距离是什么。
根据实际测试,本题中的平面距离其实指的就是欧几里得距离。
由于其 $d \leq 4$,我们就可以直接暴力枚举。
下面是一张图,代表着我们这道题某个点在不同的 $d$ 时需要连边的范围:
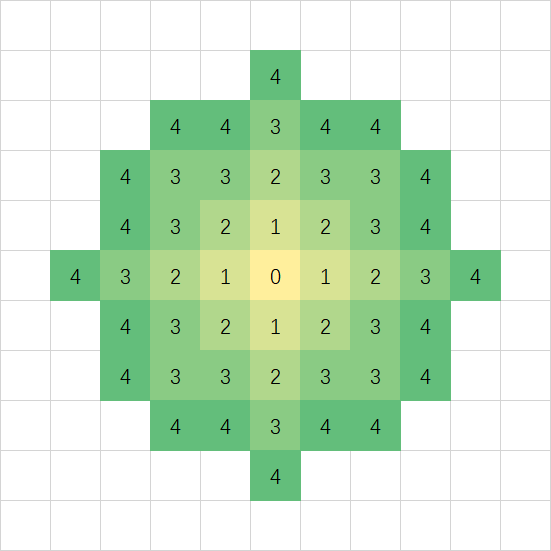
然后处理题目所给的信息:
石柱的高度就是当前点的容量,所以我们需要拆点;
跳出地图外面了就代表可以连向汇点;
有蜥蜴就代表着可以连向源点。
然后就跑最大流,得到的是可以逃离地图的蜥蜴个数的最大值,输出蜥蜴总数与其之差即可。
[USACO07OPEN] Dining G
P1402、P2891和P1231实质上是一类问题,都是三种物品进行匹配,求最大匹配个数。
对于这类问题,我们的思路就是拆点。
将匹配的主体(比如P2891的奶牛、P1402的顾客和P1231的练习册)拆成两个点,中间连一条容量为1的边,然后两个点分别与剩下的两种物品连边,然后跑最大流即可。
主主树
经典题目。
我们需要思考一下为什么图中箭头指向的是输的一方。
加入我们按照这个思路,每一个byx的人都向能够赢的诗乃的人连一条边,这就是一个新的图。
我们想要找到最大的边集,使得边集内的边两两不共用端点,最后我们求出的边集的大小就是byx可以赢的场数。
那我们考虑对这张图建立网络流模型。
我们首先把原图中的所有边建立起来,容量为1。
然后把所有byx的人连向源点,所有诗乃的人连向汇点。这样每一个流量就代表byx能赢的一场。
然后我们需要限制点的访问次数,我们可以拆点。
然后就跑最大流即可。
注意我们需要将得到的最大流量与比赛的场次取min再输出,最后才是真正能赢的场数。(没比赛你赢个什么)
[CQOI2014] 危桥
往返算经过两次,所以我们可以将危桥所说的“经过两次”转化为“往返一次”。
然后,危桥只能往返一次,普通桥能往返无数次,两个人分别想要往返 $a_n$ 次和 $b_n$ 次。
于是我们就可以将一次往返当做一单位的流来走,$a_1$ 和 $b_1$ 连源点,$a_2$ 和 $b_2$ 连汇点,最大流就是能往返的最大次数。
但是这样会忽略一些问题:从 $a_2$ 流出的流到底是来自 $a_1$ 的还是来自 $b_1$的?同理,从 $b_2$ 流出的流到底是来自 $a_1$ 的还是来自 $b_1$的?
我们考虑反向跑一遍,只不过只针对于Bob。
这次我们将$a_1$ 和 $b_2$ 连源点,$a_2$ 和 $b_1$ 连汇点,最大流看是否还与上一次相等。
如果两次均等于 $a_n+b_n$ 的话,那么两人的愿望就可以达成,否则就不可以。
二分图
[USACO05NOV] Asteroids G
我们如果想要消除一颗小行星,那么其肯定在列上或者行上有布置过一次武器,或者两者兼有。
那么,每一颗小行星就可以对应二分图上的一条边,我们就需要找一个点集,使得所有边的两个端点之一在这个点集中。
这便是二分图最小点覆盖。
我们就可以用二分图最大匹配来解决这个问题。
最小割
SAC E#1 - 一道难题 Tree
这道题要求我们求出使任何叶子结点与根节点不连通的最小代价。
我们可以转化一下。
我们可以知道,如果我们要求任何叶子结点都与根节点不连通,那么从根节点到每一个叶子结点的路径上面一定被割开过边。
我们还需要让费用最小,那么我们最多每条路径上割开一条边。
于是我们就可以用最小割来求解。让根节点连上源点,所有叶子结点连上汇点,然后跑最小割即可。
[USACO5.4] 奶牛的电信 Telecowmunication
题目要求我们求出,我们需要删除多少个点才能使题目给出的两个点之间不连通。
我们之前只做过割边的题目,没有做过这种题目,考虑将其转化一下。
方法很简单,就是拆点。
我们可以将删除点改为删除连接被拆的点的两部分的边,这样就可以转化为割边的问题了。
然后建图,原图中的边容量均为无限大,拆点得到的边的容量均为1即可。
然后跑最小割。
[SHOI2007] 善意的投票 / [JLOI2010] 冠军调查
题目告诉我们,我们需要求出来冲突数量。
我们先分析冲突的产生。
冲突之所以会产生,其根本原因就在于与自己至少一个好朋友的政见不合。他们要么违反自己的意愿而产生一单位的冲突,要么违反好朋友的意愿而产生一单位的冲突。
其中第一种冲突完全是由于第二种冲突而产生的。
如果这里没有好朋友关系,那么就不会有好朋友之间政见不合而导致的冲突了。
而第二种冲突呢?
来源是一对好朋友之间要求与对方持相同政见。
如何解决第二种冲突?
简单,不再持自己的立场或者不再为好朋友关系即可。
于是我们就可以连边了。
每一对好朋友之间连双向边,然后每一个小朋友向自己的立场(源点与汇点之间自己看着选)连一条边。容量均为1。
然后跑最小割即可。
[CEOI2008] order
如果不考虑租的情况的话就是最大权闭合子图问题了。
因为工作和租用的机器是一一对应的,所以我们也可以用一条边来代表这个关系,而这种边也得可以是被割掉的才可以。
那么我们可以把工作和对应的机器连起来,边权是租用的费用。
这种边割断了之后也可以使源点和汇点不连通,割掉了代表我们对于这个工作是租用机器的。
其余的还是正常的最大权闭合子图问题,只不过原图中的边已经建好了,我们就不需要再建了。
小M的作物
如果我们不考虑组合之间的关系,只考虑每一个作物种在哪里,我们可以把每一个作物抽象成点,然后从源点连向该点,容量为 $a_i$,该点连向汇点,容量为 $b_i$。
以这张图跑最小割的话,我们可以知道
费用流
[NOIP2000 提高组] 方格取数
每一个点向其右侧和下侧的两个点分别连边,同时每个点拆点,容量为2,边权为方格中的数。
$(0,0)$ 连向源点,$(n,n)$ 连向汇点。
然后跑最大费用最大流即可。
[NOIP2008 提高组] 传纸条
每一个点向其右侧和下侧的两个点分别连边,同时每个点拆点,容量为1,边权为好感度。
$(0,0)$ 连向源点,$(n,m)$ 连向汇点。
然后跑最大费用最大流即可。
[SDOI2006] 仓库管理员的烦恼
我们想要找到的是一种方案,使得每一种货物能够以最小的代价各自被分到一个单独的仓库里面。
但是题目并不需要我们输出具体的方案,只需要我们输出最小代价。
因为本仓库的物品再运回到本仓库是不会产生代价的,所以我们每一个仓库运送货物的代价都可以表示为运进该仓库的商品的代价之和,这等于所有该类商品的数量之和减去当前仓库内的该种商品总数。
于是我们建立 $2n$ 个点,一半代表仓库,一半代表货物种类。
每一个仓库都向所有的货物种类连一条容量为1,费用为所有该类商品的数量之和减去当前仓库内的该种商品总数。
然后跑费用流即可。
[HAOI2010] 订货
我们考虑以每月仓库的状态来建立节点。
每个节点都从源点连一条边,容量为无限,费用为 $d_i$,代表进货;
同时每个节点都向汇点连一条边,容量为 $U_i$,费用为0,代表供应市场;
每个不是最后一个节点的节点都向其下一个节点连一条边,容量为 $S$,代价为 $m$,代表存贮。
最后跑最小费用最大流即可。
[SDOI2009] 晨跑
将十字路口抽象为节点,将街道抽象为边。
这道题就不需要我们另建源汇点了,题目中已经给出了源汇点。
一个周期就相当于是从源点到汇点的一个流,路程就相当于是其代价。
于是就建边,跑最小费用最大流。
上下界网络流
[JSOI2013] 旅行时的困惑
如果我们想让任意两个岛屿都可以互相到达,那么我们需要在原有的树的基础上面建立一棵有双向边的树。
这样我们就可以建立一个上下界网络流的模型。
建立原树边的反向边,容量范围为 $[1,\infty]$。
因为一条交通线路从任意一个点开始或结束都可以,所以每一个点都从源点连边,向汇点连边,容量均为 $\infty$。
然后就跑有源汇有上下界最小流即可。