虚树
虚树。
虚树,顾名思义,是一棵树。
有时候题目给的树太大了,同时每一次处理询问的时候总会有大量的不可避免的冗余信息需要处理,这时候就需要我们对当前的树建立一棵虚树来选择性地忽略掉一些不重要的信息,进而减小了时间复杂度。
一般需要建立虚树的题目会在树上选择出几个关键点进行询问,而不关心其它的信息。同时我们还可以注意到,关键点的个数一般是与树的大小是同阶的(即在同一个数量级内)。这指的是,假如我们每一次询问的关键点个数是 $k_i$ 个,一共有 $m$ 次询问,那么 $\log_{10} (\sum k_i) = \log_{10} n$。
引子
比如说这道题:
Luogu P2495 [SDOI2011] 消耗战
这一道题需要我们找到使所有关键点都不与根节点连接的割边方案,并且需要使这个割边方案中边的权值和最小。
对于这个问题,我们有一套经典的DP方案:
设 $dp[u]$ 表示使编号为 $u$ 的点不与其子树中任意一个关键点联通的最小代价。
设 $w(i,j)$ 表示连接 $i$ 与 $j$ 的边的权值。
那么我们可以枚举 $u$ 的儿子 $v$:
- 若 $v$ 不是关键点,那么 $dp[u]=dp[u]+\min(dp[v],w(u,v))$;
- 若 $v$ 是关键点,那么 $dp[u]=dp[u]+w(u,v)$。
单次DP的时间复杂度是 $O(n)$ 的。因为题目给出了 $m$ 次询问,并且每一次询问时关键点的信息还会改变,所以我们每一次询问的时候必须得重新DP一遍,这让我们总体的时间复杂度成为了 $O(nm)$。
然后看题目要求:
对于 $100\%$ 的数据,$2\leq n \leq 2.5\times 10^5, 1\leq m\leq 5\times 10^5, \sum k_i \leq 5\times 10^5$。
我们一眼就可以看出来以 $O(nm)$ 的复杂度是绝对过不去的。
经试验验证(LibreOJ),以下面的代码可以跑出来50分的好成绩:提交寄录
虚树
我们重新来看一遍DP的过程。
我们在枚举某一个节点的所有儿子的时候,假设这个节点 $u$ 下面的子树内没有一个关键点,那么这个DP的过程就是冗余的。
既然我们不需要 $u$ 及其子树的信息了,那么它也就没有了继续存在于图内的必要了。
而如果 $u$ 下面的子树内有关键点,那么他也不一定能留下。
鉴于我们只关心关键点之间的连通性,我们关心的只有两类点:一是关键点,二是可能是两个关键点的LCA的点。
前者的数量是给定的,而后者只会在树分叉的地方出现,数量不会大于关键点的个数。
我们就可以对这两种点建立一棵新的树,而树上的边权就是我们关心的信息——在这道题内就是两端点在原树上的路径中的最小边权。
然后我们就可以对着明显缩水了的树进行DP了。
如果我们使用正确的求LCA算法的话(比如 $O(\log n)$ 的树剖),我们的时间复杂度就是 $O(\log \sum k_i)$ 了。
而由于 $\sum k_i$ 与 $n$ 同阶,所以我们可以近似的将我们的时间复杂度看为 $O(n \log n)$。
建立
既然有了思想,我们就可以着手建立虚树了。
我们当然不可能逐个枚举关键点的LCA并加进去来建立,这样的复杂度仍然是 $O(k^2)$ 级别的,我们无法接受。
我们需要尝试将这个算法优化,至少优化到 $O(k)$ 级别(不算LCA的 $O(\log n)$),这样我们才能够通过上面的数据范围。
自己手模一下,可以发现LCA只会在树分叉的地方出现,所以我们只需要维护树分叉的地方就可以了。
那怎么维护呢?
我们可以尝试维护极右链。
对于这样的一棵树:
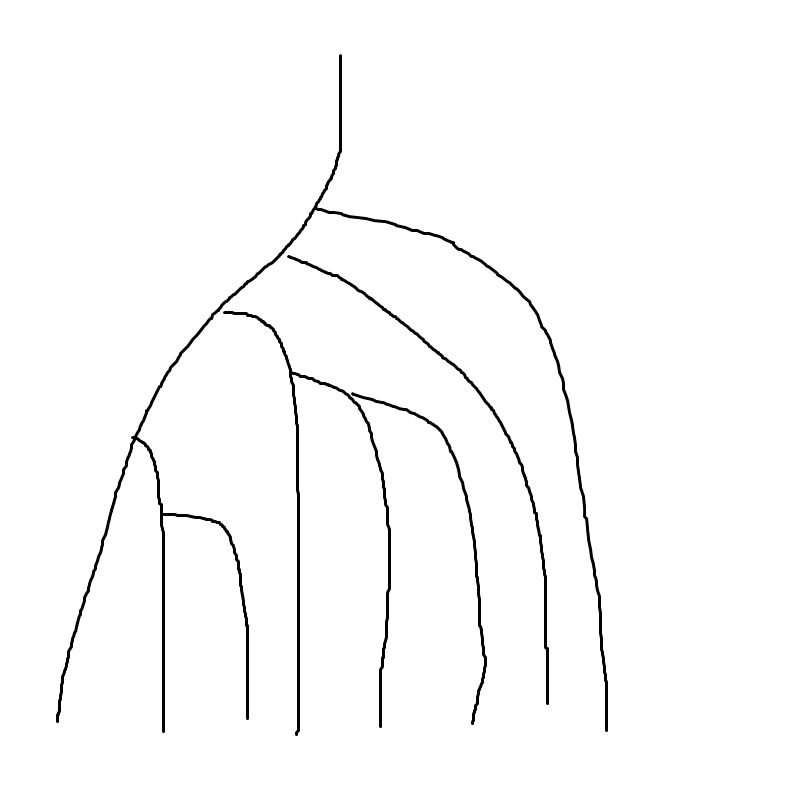
现在它的极右链是这块红色的链:
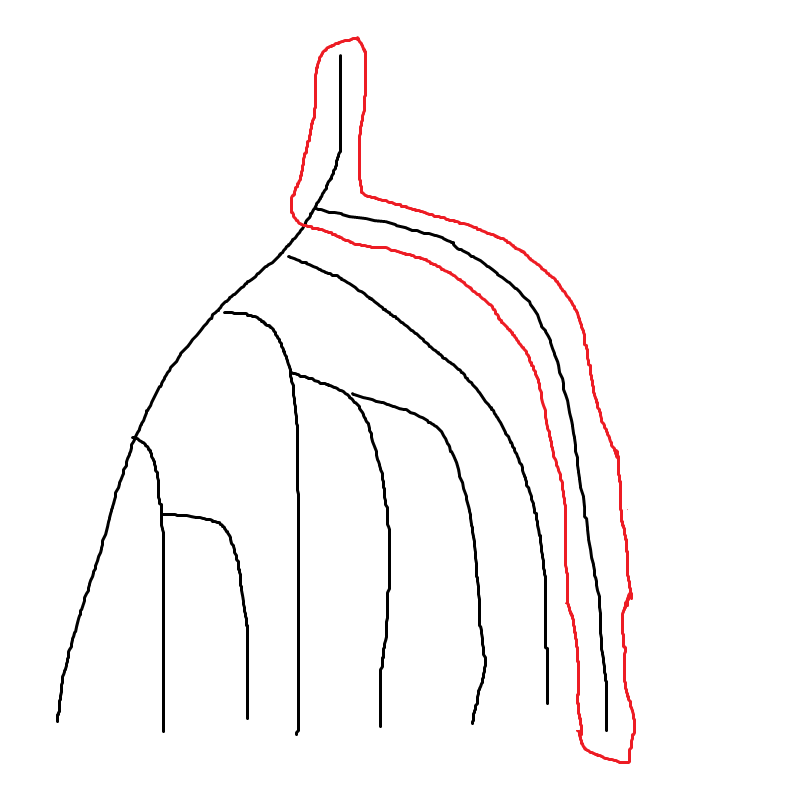
那么假设我们最后的点是这个红色点,美剧导的下一个点是这个蓝色的点:
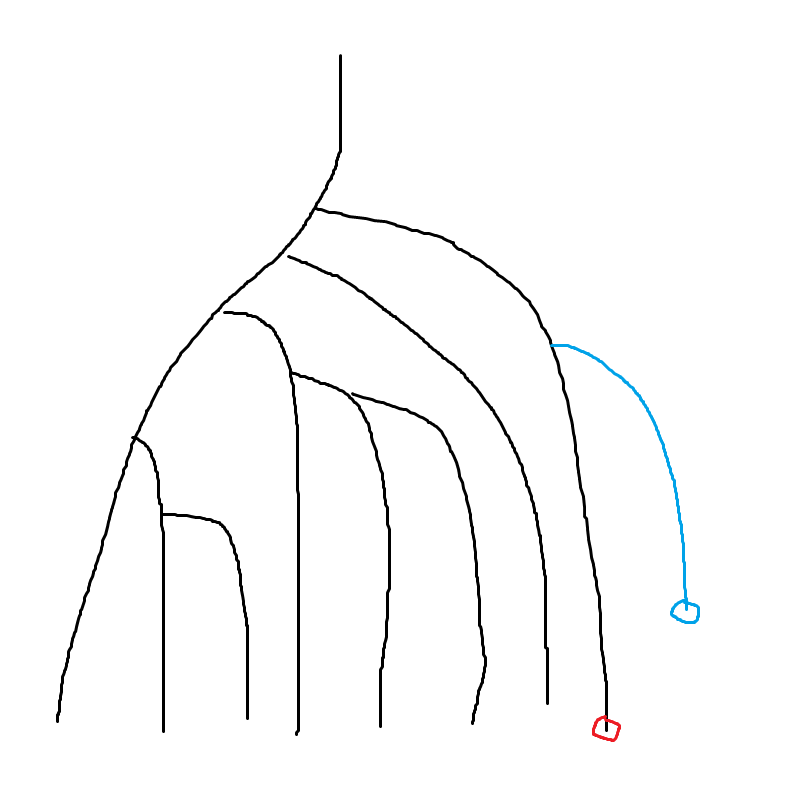
蓝色的点向上到根节点的路径有与之前已经建好了的树重合的部分,也有之前没有出现过的部分(蓝色的链)。
我们把这个点加入树中的同时,还需要加入它与之前的极右链中的交点,即其与上一个关键点的LCA。
然后,最新的极右链就是这个:
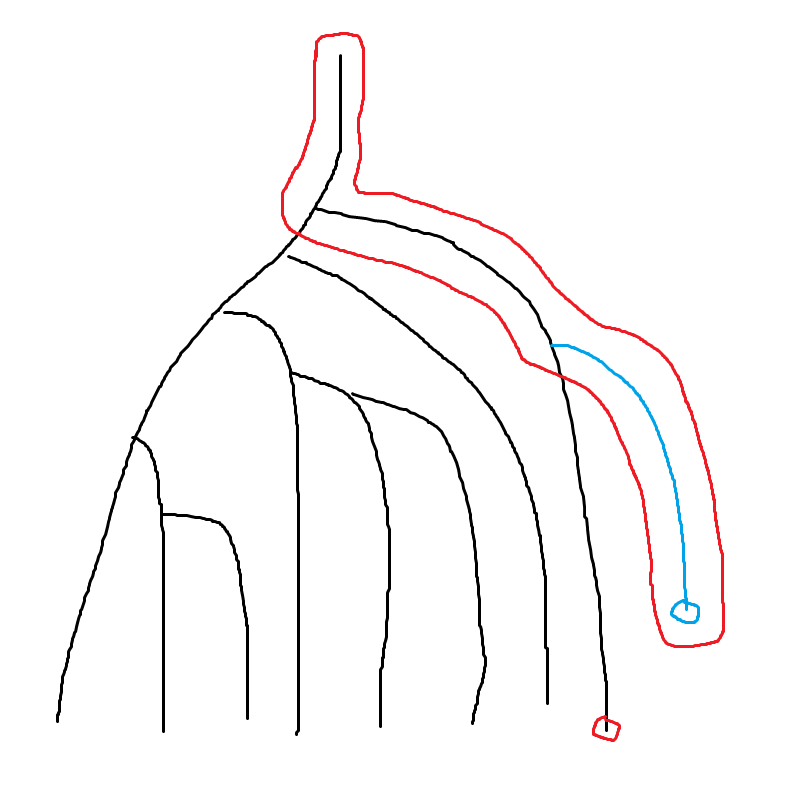
为了保证不会损坏虚树的结构,首先我们将所有的关键点按照DFS序来排序,保证逐个遍历的时候不会有新的关键点出现在当前极右链的左边。
然后我们使用栈来维护遍历的顺序,就像我们DFS时的系统栈一样,记录下之前遍历的点。
下面的代码里面的注释就是对该步骤的解释:
1 | void build() |
然后就可以愉快地在虚树上进行dp了,方法与之前一样。
现在我们的复杂度大大减小,就可以拿到——80分的好成绩!提交寄录
然后我们就不理解了。
我的理论复杂度也是对的,应该没有什么问题。
我们回忆一下我们代码的实现:
我们在每一次建立虚树之前,都把整个链式前向星都清空了一遍。
这时我们可以再懒一点,我们可以不需要清空链式前向星,只需要将每一个入栈的节点在入栈的时候清空该节点的表头即可。
1 | void build() |
剩下的节点我们就不需要管了,因为我们甚至没有访问他们的机会。
例题
Luogu P2495 [SDOI2011] 消耗战
题面在这里:https://www.luogu.com.cn/problem/P2495
上面已经讲了做法了,就是一个树形DP。
代码见这里:Luogu P2495