Trie 与 AC自动机

发表于 2022-04-05 更新于 2022-11-09 分类于字符串本文字数： 3178 阅读时长 ≈ 8 分钟

Trie树（字典树）与AC自动机。

Trie

Trie树，又称字典树，是一种数据结构。

Trie树可以存储大量不同的字符串，同时支持对其以 $O(|S|)$ 的复杂度进行查询。

首先我们可以放一张图上来：

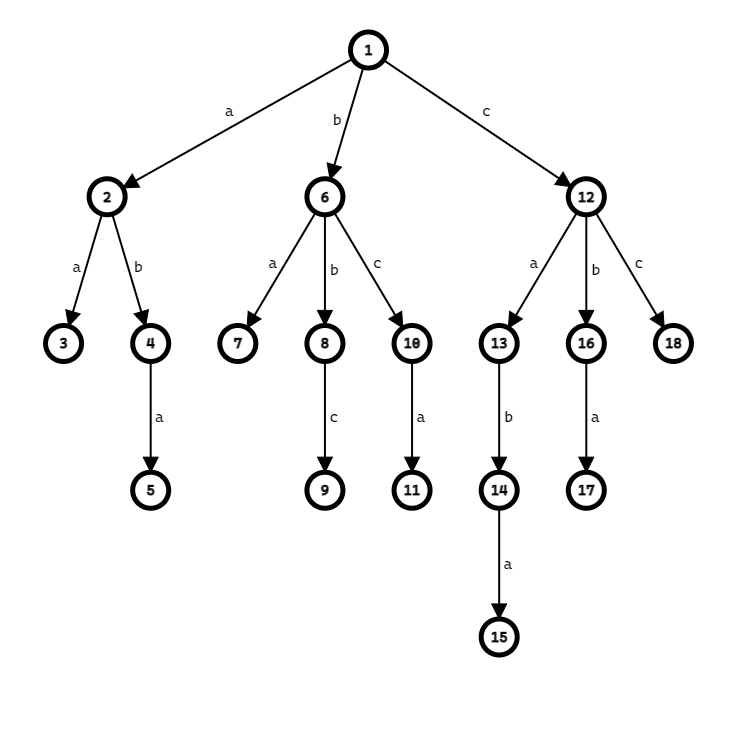
这就是我们向Trie中顺序插入了aa,aba,ba,bbc,bca,caba,cba,cc八个字符串之后的结果。

我们可以发现，Trie使用边来代表字母，而用点来表示字符串。
某一个点表示的字符串就是从根节点到该节点的路径上的字母顺序排列组合而成的字符串。
比如说17号节点就代表着cba这一个字符串。

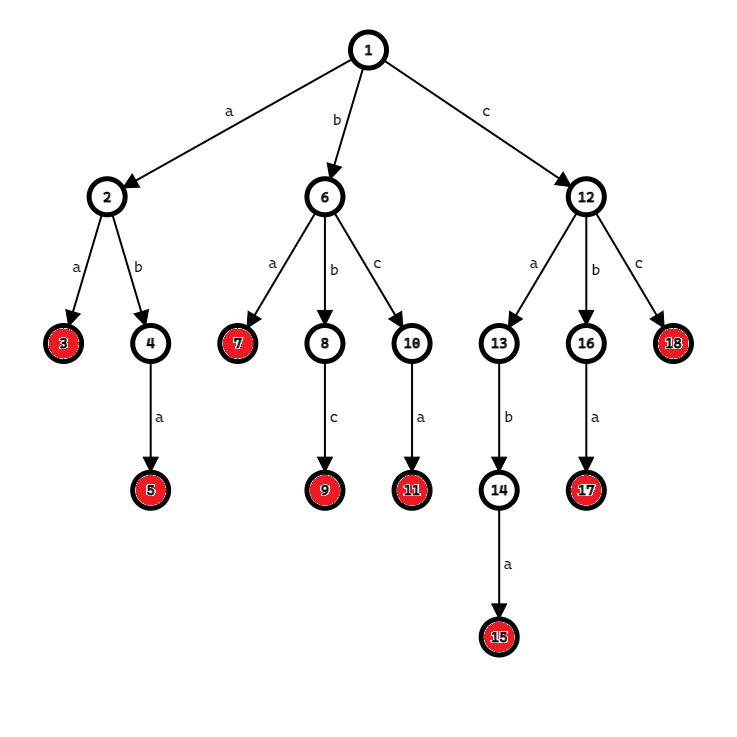
每一个点虽说都代表着一个字符串，但是这个字符串不一定被插入过。我们将实际上有的字符串进行了标红。

实现

存储

我们将每一个节点存储到一个结构体里面：

数组
指针

struct trie
{
    int s[26];
    int cnt;
}tr[N];

struct trie
{
    trie *s[26];
    int cnt;
}tr[N];

这里 s 数组的大小是根据字符集的大小来定的，一般情况下是小写字母集，所以这里填的是26。

插入

具体思想就是，如果当前节点的下一位所对应的儿子非空就跳到对应的儿子，是空的那就新建一个儿子。

数组
指针

void insert(string s)
{
    int u = 0;
    for(int i = 0; i < s.length(); i++)
    {
        if(tr[u].s[s[i] - 'a'] != 0)u = tr[u].s[s[i] - 'a'];
        else
        {
            tr[u].s[s[i] - 'a'] = ++idx;
            u = idx;
        }
    }
    tr[u].cnt++;
}

void insert(string s)
{
    auto *u = &tr[0];
    for(int i = 0; i < s.length(); i++)
    {
        if(u->s[s[i] - 'a'] != 0)u = u->s[s[i] - 'a'];
        else
        {
            u->s[s[i] - 'a'] = &tr[++idx];
            u = u->s[s[i] - 'a'];
        }
    }
    u->cnt++;
}

删除

删除这个操作使用的范围不是很广。具体思想就是将对应我们想要删除的字符串的点的cnt值减去1即可。

数组
指针

void loeschen(string s)
{
    int u = 0;
    for(int i = 0; i < s.length(); i++)
        u = tr[u].s[s[i] - 'a'];
    tr[u].cnt--;
}

void loeschen(string s)
{
    auto *u = &tr[0];
    for(int i = 0; i < s.length(); i++)
        u = u->s[s[i] - 'a'];
    u->cnt--;
}

查询

查询操作的思想就是，不断从根节点沿着字符串跳，直到调到空节点或者跳完整个字符串为止。

数组
指针

bool chq(string s)
{
    int u = 0;
    for(int i = 0; i < s.length(); i++)
    {
        if(tr[u].s[s[i] - 'a'] != 0)u = tr[u].s[s[i] - 'a'];
        else return false;
    }
    return tr[u].cnt > 0;
}

bool chq(string s)
{
    auto *u = &tr[0];
    for(int i = 0; i < s.length(); i++)
    {
        if(u->s[s[i] - 'a'] != 0)u = u->s[s[i] - 'a'];
        else return false;
    }
    return u->cnt > 0;
}

struct trie
{
    int s[26];
    int cnt;
}tr[N];
int idx = 0;
void insert(string s)
{
    int u = 0;
    for(int i = 0; i < s.length(); i++)
    {
        if(tr[u].s[s[i] - 'a'] != 0)u = tr[u].s[s[i] - 'a'];
        else
        {
            tr[u].s[s[i] - 'a'] = ++idx;
            u = idx;
        }
    }
    tr[u].cnt++;
}
void loeschen(string s)
{
    int u = 0;
    for(int i = 0; i < s.length(); i++)
        u = tr[u].s[s[i] - 'a'];
    tr[u].cnt--;
}
bool chq(string s)
{
    int u = 0;
    for(int i = 0; i < s.length(); i++)
    {
        if(tr[u].s[s[i] - 'a'] != 0)u = tr[u].s[s[i] - 'a'];
        else return false;
    }
    return tr[u].cnt > 0;
}

struct trie
{
    trie *s[26];
    int cnt;
}tr[N];
int idx = 0;
void insert(string s)
{
    auto *u = &tr[0];
    for(int i = 0; i < s.length(); i++)
    {
        if(u->s[s[i] - 'a'] != 0)u = u->s[s[i] - 'a'];
        else
        {
            u->s[s[i] - 'a'] = &tr[++idx];
            u = u->s[s[i] - 'a'];
        }
    }
    u->cnt++;
}
void loeschen(string s)
{
    auto *u = &tr[0];
    for(int i = 0; i < s.length(); i++)
        u = u->s[s[i] - 'a'];
    u->cnt--;
}
bool chq(string s)
{
    auto *u = &tr[0];
    for(int i = 0; i < s.length(); i++)
    {
        if(u->s[s[i] - 'a'] != 0)u = u->s[s[i] - 'a'];
        else return false;
    }
    return u->cnt > 0;
}

例题

Luogu P2580：https://www.luogu.com.cn/problem/P2580

参考代码：Luogu P2580

01-Trie

01-Trie是Trie的一种变体。其字符集不是一般见到的Trie的小写字符集，而是 $\lbrace 0,1 \rbrace$。

由于01-Trie的字符集仅限于0和1，所以它被人们用来处理一些与位运算有关的东西，比如说异或和或者集合内数字两两异或的极值什么的。

异或极值

我们假定我们需要维护这样一个操作：
给出一个集合 $A$，再给出一个数 $k$，我们需要在集合内找到一个数 $a_i$，使之与 $k$ 的异或值最大（或最小）。

因为异或操作就是将两个数按照二进制逐位进行比对，相同为0，不同为1，所以我们就可以将上文提到的那个集合 $A$ 内的所有数根据二进制位分解之后再插入Trie中。

然后我们就像查找字符串一样，将 $k$ 进行二进制分解后得到的01串放进去匹配。
如果我们需要的是异或最小值的话，就按照正常查找字符串的方式跳。
如果我们需要的是异或最大值的话，就让每一次跳儿子的时候跳到与当前位置不同的儿子。

我们还需要注意一点，就是我们需要保证这棵Trie的深度与数据范围的最大二进制位数一致。

由于我们是从高位到低位建的，而高位远比低位重要，所以我们就可以大胆贪心，能跳就跳，不能跳就跳到相反的那个儿子上。而且我们保证了Trie的高度是一定的，这就保证了我们一定可以跳到底。

例题

Luogu P4551 最长异或路径

参考代码：Luogu P4551

可持久化Trie

有的时候题目要求我们能够随时访问某个历史版本，或甚至回溯到某个历史版本并对其进行修改。

暴力的做法是每一次都开一个新的Trie。

这时候，我们就可以将Trie持久化以完成这些题目的要求。

之前我们每一次插入的时候都是从根节点开始的，添加的字符串也是一条从根节点开始的路径，所以我们每一次插入只需要增加新的一整条路径，并把这条路径与上一个版本中未被更新的部分连接上即可。

例题

AcWing 256. 最大异或和

参考代码：AcWing 256

AC自动机

这个AC自动机啊，他是 Aho-Corasick Automaton，不是什么Automation。

（博客的标题来自于俄语 Ахо-Корасик автомат -> Aho-Korasik avtomat）

AC自动机就像是Trie和KMP的结合。
AC自动机基于的是Trie，同时其匹配字符串时的行为与KMP有异曲同工之妙。

思想

改造 Trie

这是一个简单的Trie结构体：

struct trie
{
    int s[26];
    int cnt;
}tr[N];

对于KMP算法，我们是根据前缀函数来对字符串匹配进行优化的。
而对于Trie呢？

fail指针

我们考虑使用前缀函数的原因：

我们需要找到一个前缀，在保证其与某个后缀相等的前提下，使得当前匹配的进度最大地保留下来。

把同样的思想挪到Trie树上，我们需要找的就是：

我们需要找到一个节点，其代表的字符串是当前节点代表的字符串的最长后缀。

于是，我们就可以根据这样的情况来构建fail指针。

举个例子：

如下图，是依次向Trie树中添加he,his,him,her,hers,they,them,their,theirs,she的结果：

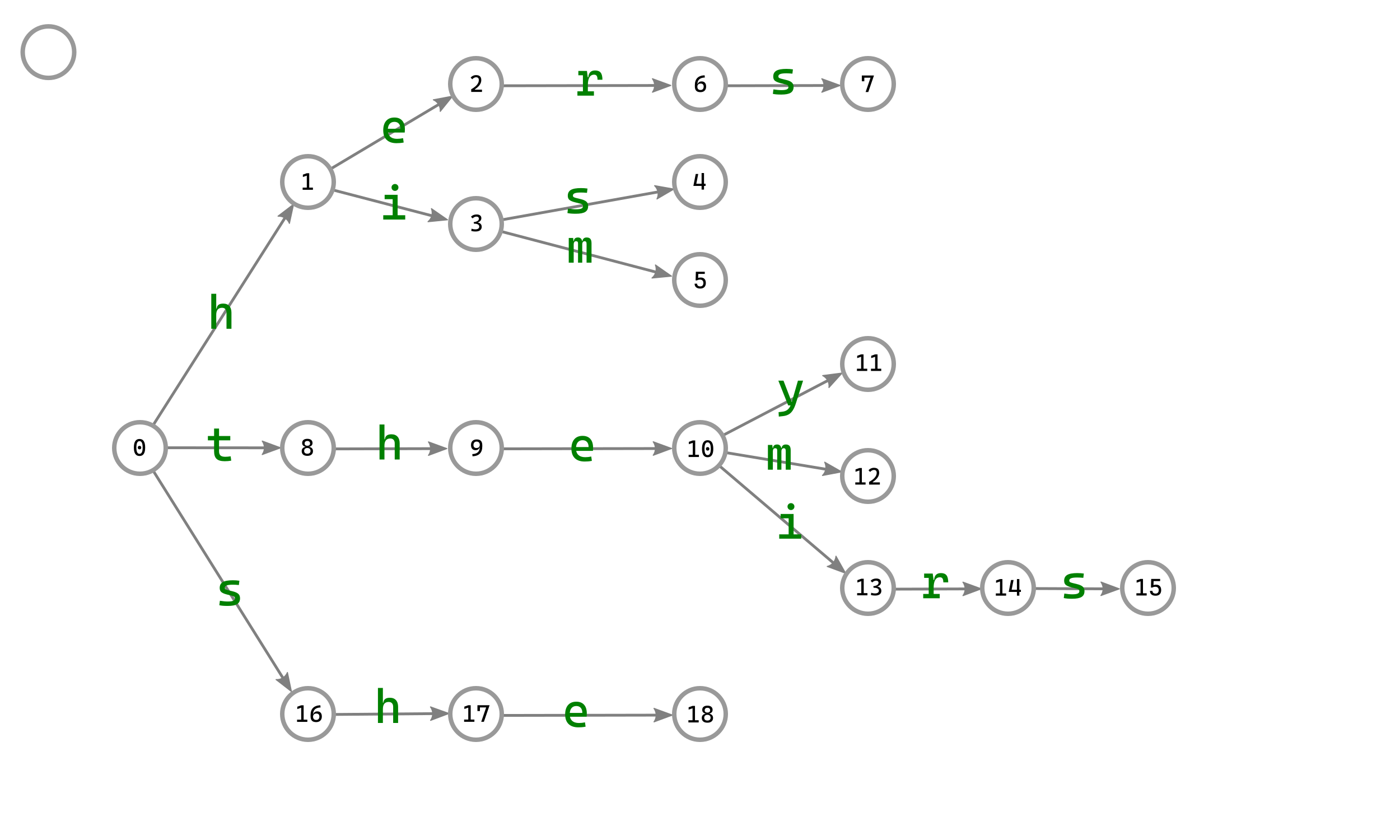
然后我们开始依次构建fail指针。

我们利用BFS来帮助我们构建fail指针。

考虑一个已经构建了fail指针的节点 $u$，其对应字符 $c$ 的儿子 $s[u][c]$ 的fail指针的构建遵循下列原则：

如果 $s[fail[u]][c]$ 存在，则让 $s[u][c]$ 的fail指针指向 $s[fail[u]][c]$。这样相当于是在 $u$ 和 $fail[u]$ 后面加一个字符 $c$，分别对应 $s[u][c]$ 和 $s[fail[u]][c]$。
如果 $s[fail[u]][c]$ 不存在，那么我们就递归寻找 $s[fail[fail[u]]][c]$，并重复上面的判断过程，直到跳到根节点。
如果真的什么都没有了，那就让 $s[u][c]$ 的fail指针指向根节点。

下图中用不同的颜色来区分不同状态的边、点：

#FF9955 代表在队列中，等待构建fail指针的点；
#FFCC00 代表正在构建fail指针的点；
#AAD400 代表已经构建完fail指针的点；

#FF0000 代表正在构建的fail指针；
#FFDD55 代表已经构建完成的fail指针。

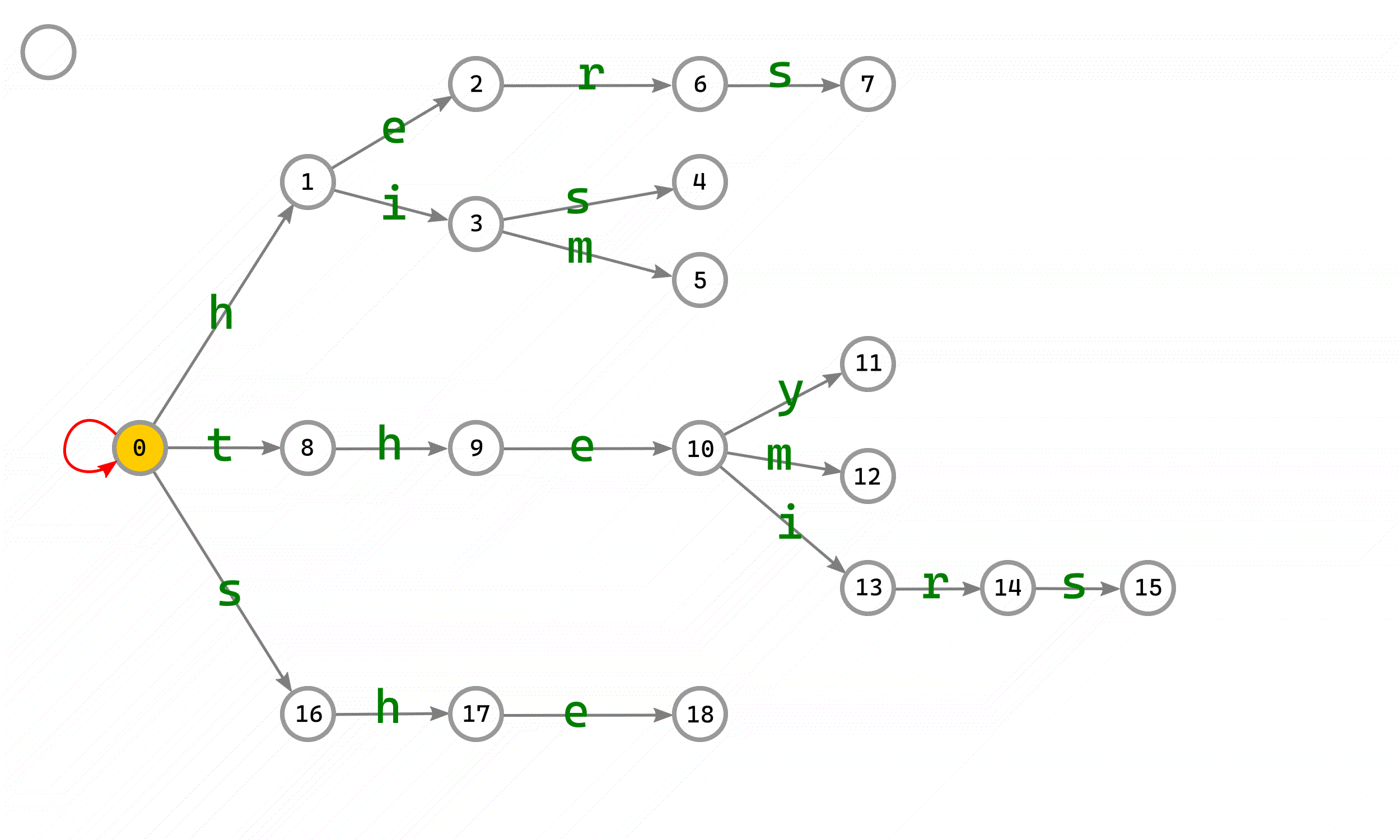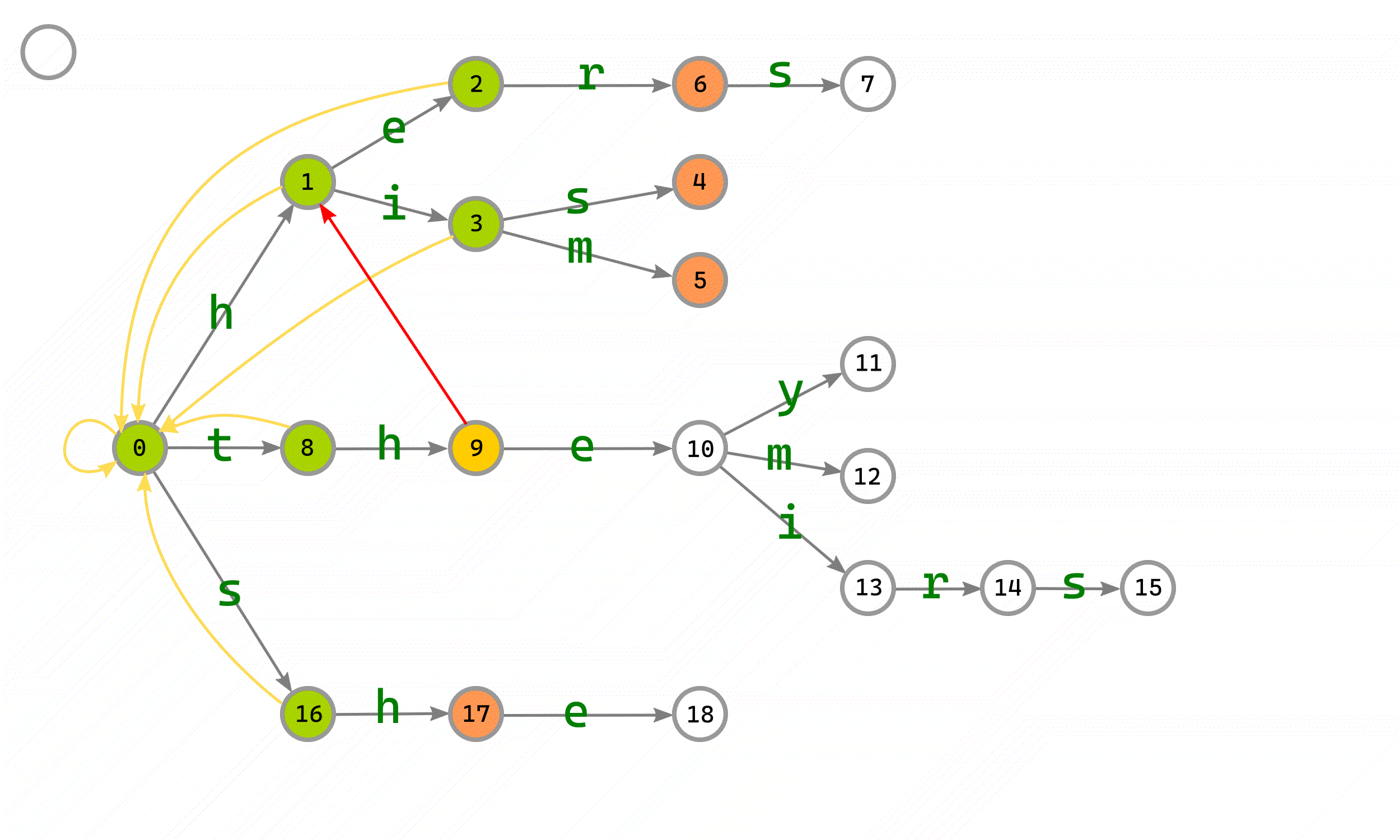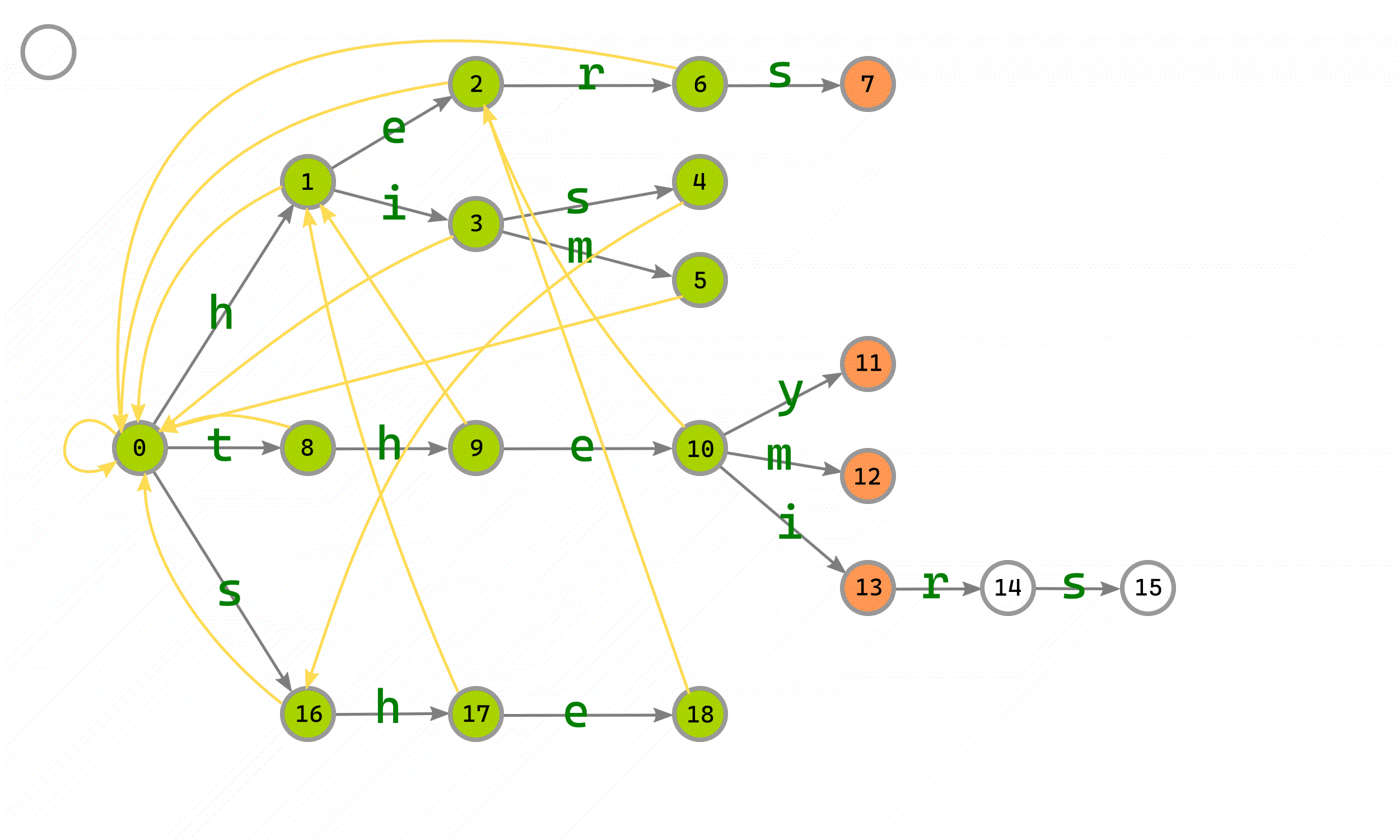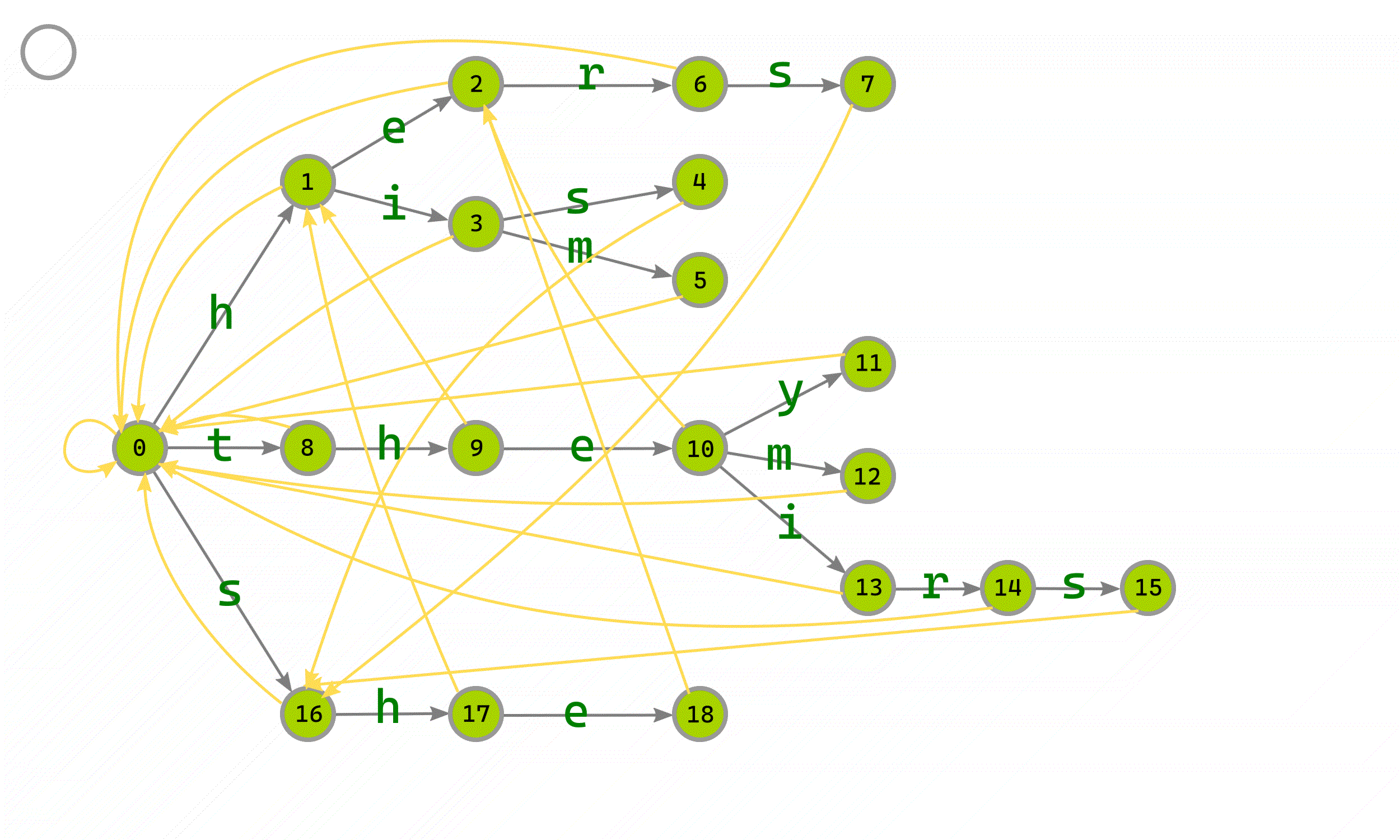
最终效果图：

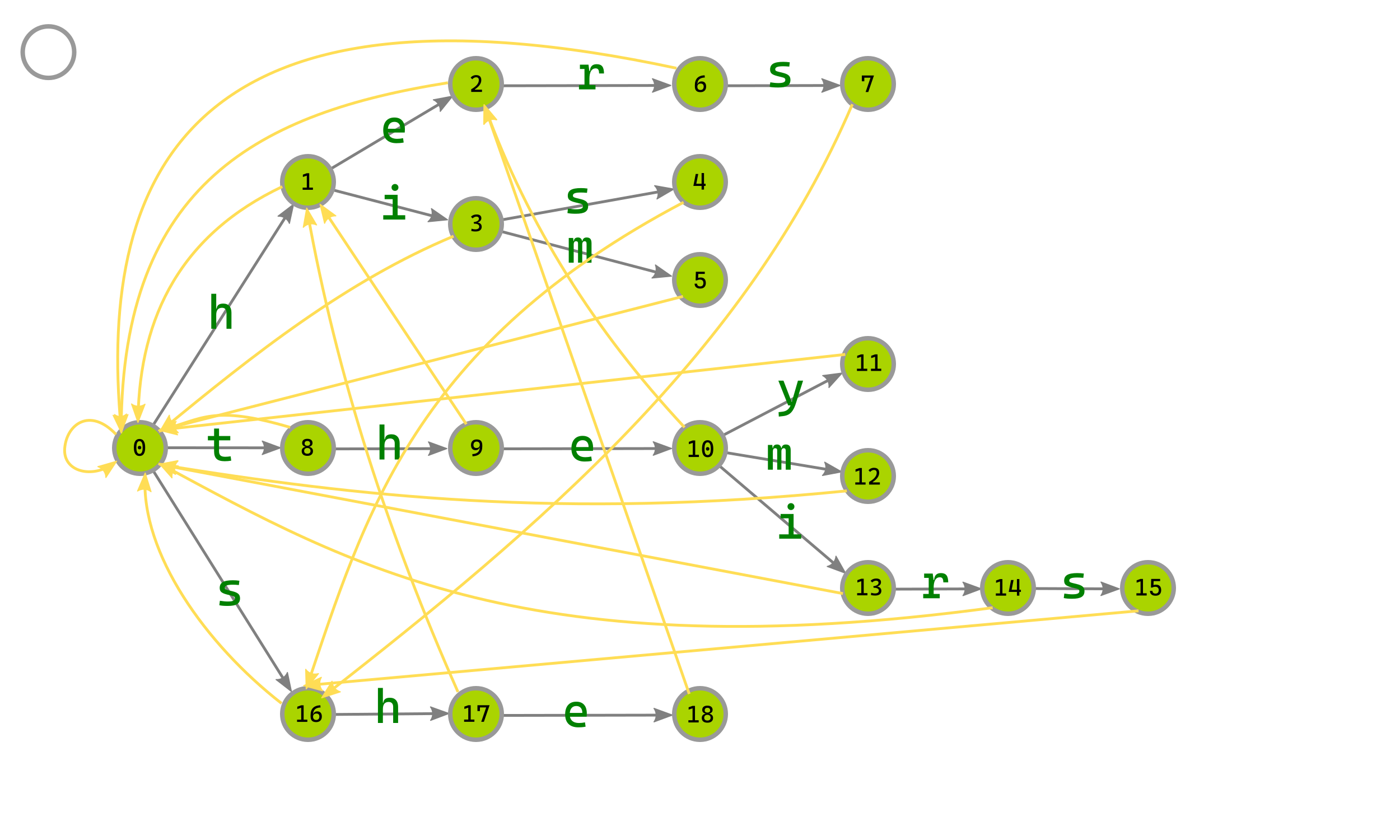
代码：

/*
struct trie
{
    int s[26];
    int cnt;
    int fail;
}tr[N];
*/
void get_fail()
{
    queue<int>q;
    for(int i = 0; i < 26; i++)
        if(tr[0].s[i])q.push(tr[u].s[i]);
    while(!q.empty())
    {
        int u = q.front();
        q.pop();
        for(int i = 0; i < 26; i++)
        {
            if(tr[u].s[i])
            {
                tr[tr[u].s[i]].fail = tr[tr[u].fail].s[i];
                q.push(tr[u].s[i]);
            }
            else
            {
                tr[u].s[i] = tr[tr[u].fail].s[i];
            }
        }
    }
}

上述代码可能与我们刚才的叙述有部分出入，原因是这份代码做了些许优化。
事实证明这些优化虽然会修改Trie的结构，使之由树变为图，但是对我们存储的信息是有利无害的。

我们首先将根节点的所有儿子入队。
如果我们第一步将根节点入队的话，会导致根节点的所有子节点的fail指针指向自己，而不是指向根节点。

然后是遍历在队列中的节点。
对于其非空的儿子，我们照常构建fail指针。由于当前节点的fail指针已经构建完毕，且沿着fail指针形成的通往根节点的链上的所有节点都已经构建完毕了，所以我们直接指向当前节点的fail指针指向的节点的所对应的儿子。如果有这个儿子的话就指向他，如果没有的话就相当于是指向根节点。

然后我们将当前节点的部分空儿子指向当前节点的fail指针指向的节点的对应儿子上。
原因就是，反正也是失配了，与其花时间判失配跳fail指针再访问，不如直接访问我们想要它到的节点。
所以我们在匹配的时候一直走（结构体意义上的）树边，直到整个跑完就可以了。

照这样建完fail指针之后，我们会将原先的Trie树变为一张“Trie图”。

由于边太多太密，我就不画了。可能会补上一张CSAcademy的图。
（太糊了，感觉会不久后撤下，就先存本地了）

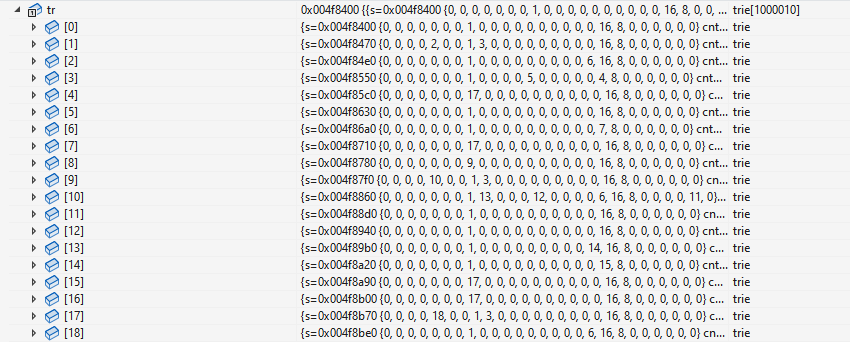
（这是原数据）

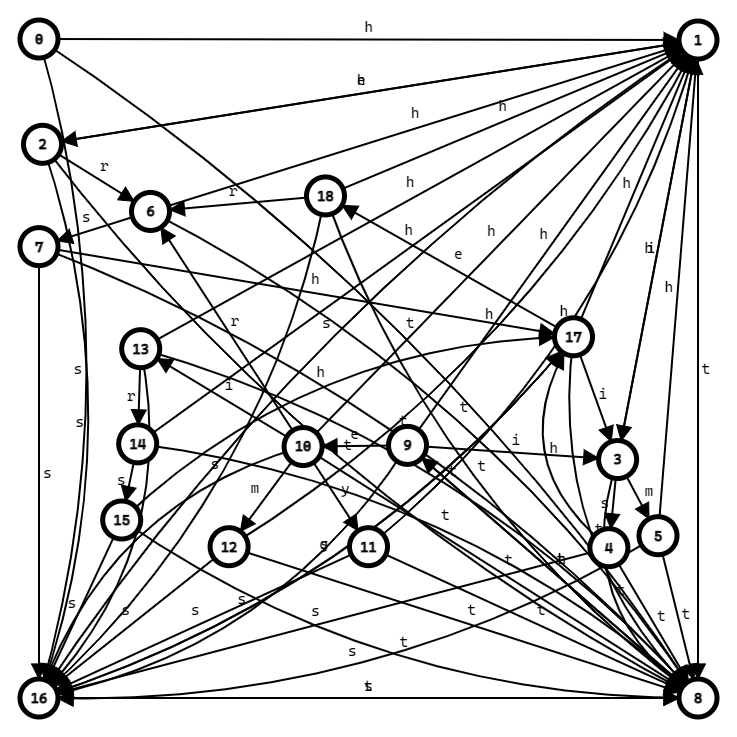
（这是图）

匹配

匹配的思路是这个样子的：

沿着Trie图的边跳，直到遍历完整个字符串为止。
由于我们在之前已经将Trie树改造为了Trie图，且fail指针已经在某种意义上失去了其作为失配指针的意义，所以我们只需要跳Trie图内的边即可。
每走到一个节点，就沿着当前节点的fail指针累加答案。
由于fail边跳到的是当前字符串在Trie内存在的最长后缀，且如果当前的模式串出现在了文本串内的话，其子串也会出现在文本串内，所以我们可以沿着fail指针一路遍历当前模式串的所有后缀。

这里有一份对于多模式串匹配，且允许模式串多次被统计的，用来统计所有模式串的总出现次数的代码：

int query(string s)
{
    int u = 0;
    int res = 0;
    for(int i = 0; i < s.length(); i++)
    {
        u = tr[u].s[s[i] - 'a'];
        for(int j = u; j > 0; j = tr[j].fail)
            res += tr[j].cnt;
    }
    return res;
}

其中res是所有模式串的总出现次数。

例题

P3808 【模板】 AC 自动机（简单版）

参考代码：Luogu P3808

P3796 【模板】 AC 自动机（加强版)

参考代码：Luogu P3796