树状数组
简介: 树状数组
树状数组
一种神奇的数据结构。
引子
当我们想要对一个数组进行单点加时,我们可以选择使用普通数组,时间复杂度是 $O(1)$;
当我们想要对一个数组进行区间求和时,我们可以选择使用前缀和数组,时间复杂度也是 $O(1)$;
但是,前缀和数组在进行单点加时,时间复杂度是 $O(n)$ ;
而普通数组在进行区间求和时,时间复杂度也是 $O(n)$ ;
我们能不能设计出一个数据结构,让我们在进行这两个操作时牺牲某一个操作的时间复杂度,而减少了另一个操作的时间复杂度呢?
于是,树状数组就应运而生。
简要介绍
树状数组的存储原理是这个样子的:
我们称原数组为 $a[i]$ ,我们正常所输入的数据就存储在这里。
在原数组 $a[i]$ 的基础上,我们创建一个新的数组 $c[i]$ 。
数组 $c[i]$ 是以这个规则存储信息的:
我们先列出所有的数组下标:
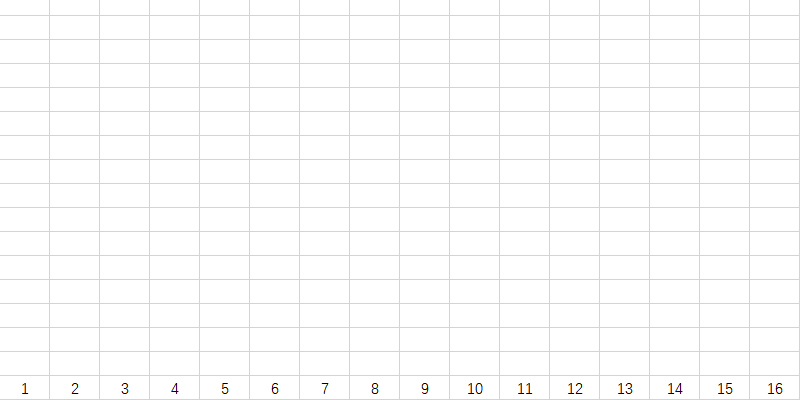
接下来我们开始考虑数字的 $lowbit$ 。
所有奇数的 $lowbit$ 都是1。
我们在第一层标记上 $lowbit$ 为1的所有数字:
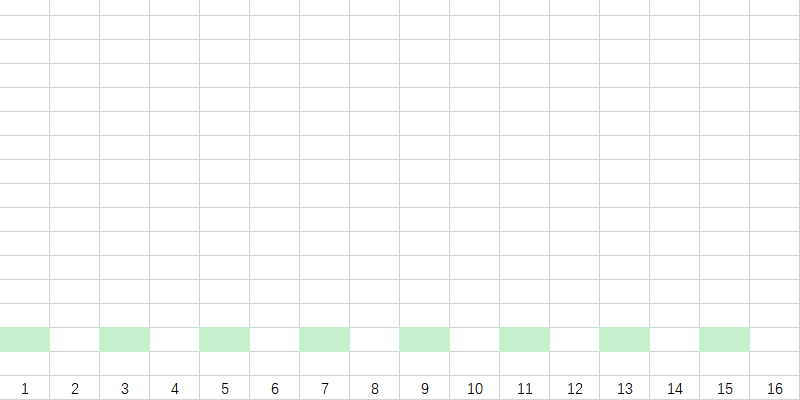
接下来,我们依次标上数字的 $lowbit$ :
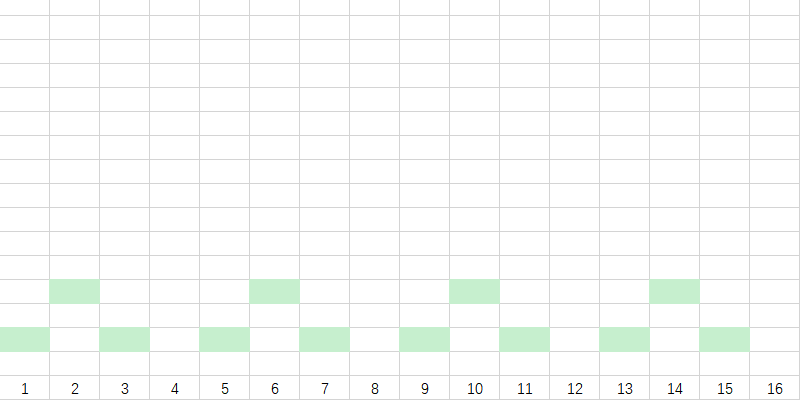
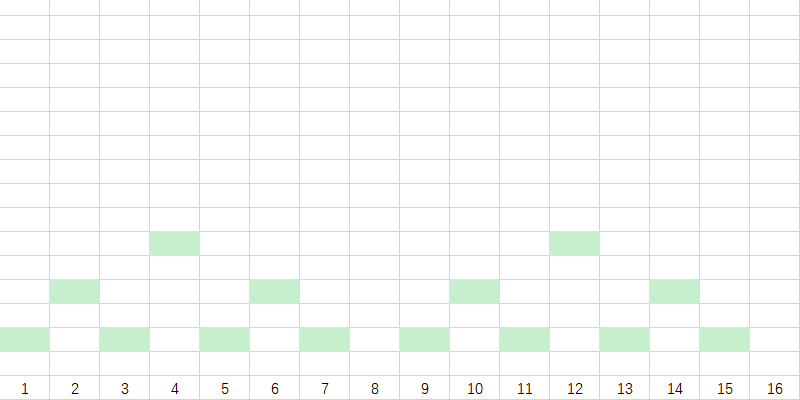
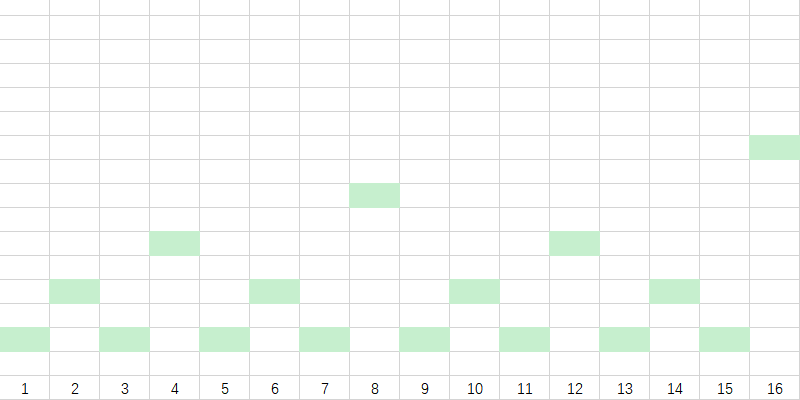
最后,我们再进行一下延长,每一个块向左延长至长度为 $2^{lowbit(i)}$ 。
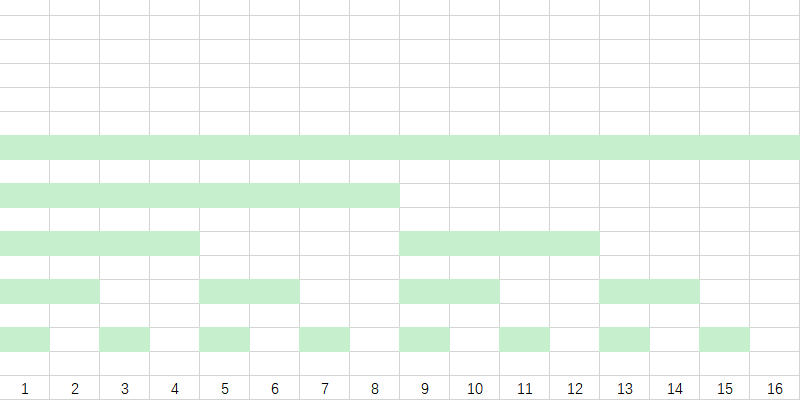
我们对块进行一下标号:
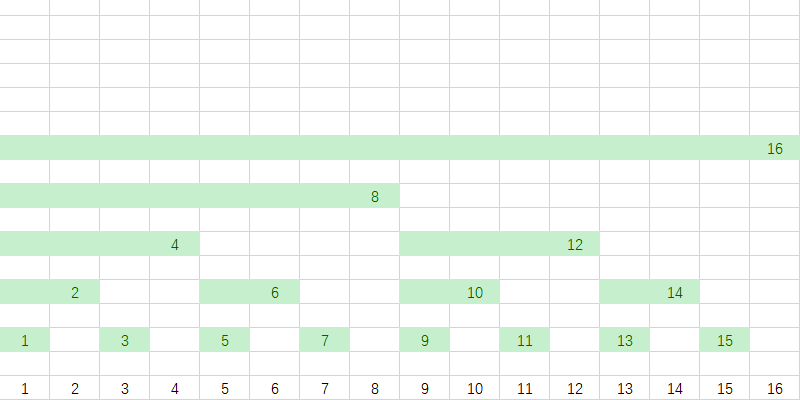
这些绿色的块里面存储的是其下方所有数字的和。
当然,我们进行值的更新的时候,不可能一个一个加起来再更新,这样复杂度又回到了原先的样子。
我们更新时遵循的是这样一个路线:
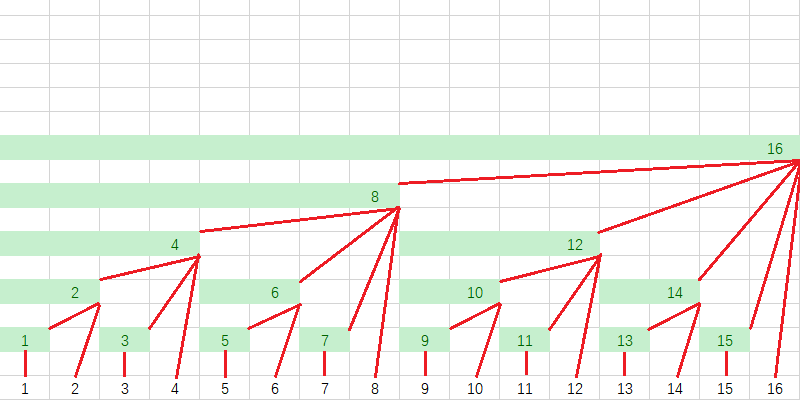
因为每一个数有 $\log (n)$ 位,所以最终两个操作的时间复杂度都是 $O(\log n)$ 。
板子
Luogu P3374 【模板】 树状数组1:https://www.luogu.com.cn/problem/P3374
示例代码:Luogu P3374