线段树
线段树及其衍生,如动态开点线段树、可持久化权值线段树等等。
什么是线段树?
线段树是一种数据结构,其可以以 $O( \log n)$ 的时间复杂度处理维护区间信息的问题。
其维护的信息满足可以快速合并两个区间的信息(例如区间和、区间最大(小)值。
线段树同时可以支持区间修改,但是区间修改时必须能够快速求出每个区间维护的信息。
线段树的结构
线段树在建立的时候,会将每一个区间长度不为1的区间进行二分,并递归对这两个区间进行判定。
这是一棵区间长度为12的线段树:
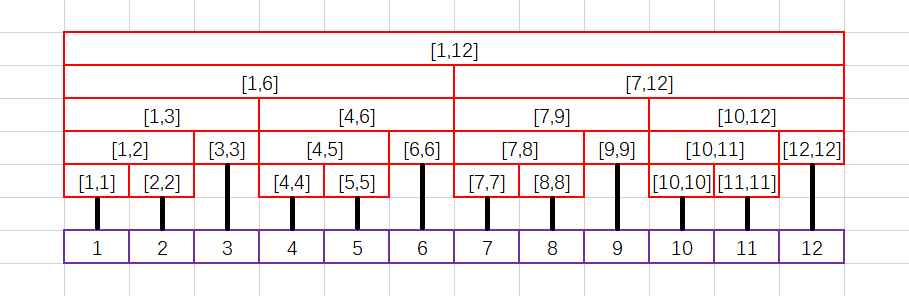
我们可以明显看到,线段树是一棵二叉树。
线段树的高度一般是 $\log n$ 的,这就需要我们建立 $2^{\lceil \log n \rceil + 1}$ 个节点,这将会耗费我们大量的空间。
一般情况下,我们为了访问方便,也为了节省空间,我们一般将一个节点(设其编号为 $p$)的左儿子和右儿子分别设为 $p << 1$ 和 $p << 1 | 1$,就相当于是在一棵满二叉树上面访问。
于是我们就给出编号:

下面给出示例代码:
假设我们维护的是区间和,并使用类似
1 | struct SegTree |
的结构体来存储数据,那么建立线段树的函数就是像下面这个样子的:
1 | void build(int p, int l, int r) |
线段树的区间询问
我们这里以区间求和为例。
我们先手动模拟一下区间求和的过程:
假设我们对这样一个长度为12的序列 $\lbrace 1,1,4,5,1,4,1,9,1,9,8,1 \rbrace$ 建立线段树,那么我们每一个区间的数据是这个样子的:
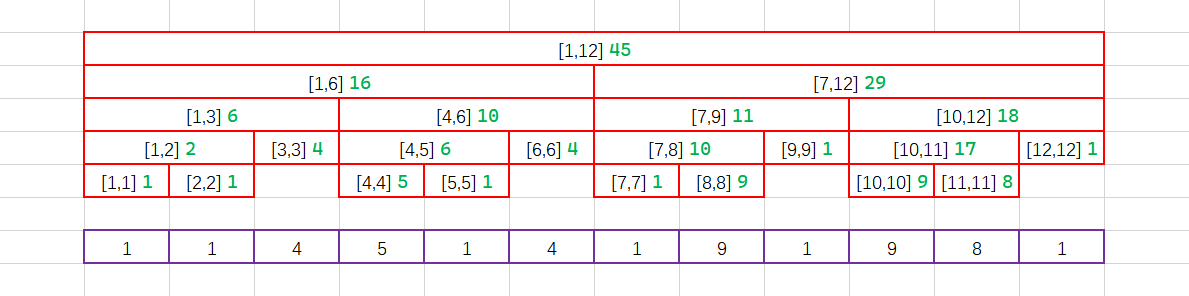
我们假设需要对 $[2,8]$ 这个区间内的数据进行求和,那么我们覆盖的区间就是这个样子的:
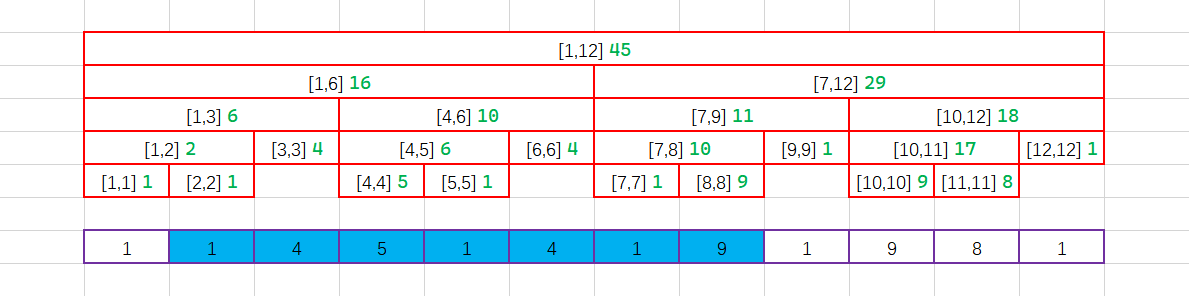
我们想象一下将区间向上推:

最后我们将 $[2,8]$ 这个大区间分为 $[2,2] \cup [3,3] \cup [4,6] \cup [7,8]$ 这几个小区间。

我们每一次二分递归的时候,如果当前区间被我们询问的区间完全包含就返回当前区间的值,如果没有完全包含就递归询问左右区间,并输出两个区间的返回值之和。
在递归询问左右两区间的时候需要注意一下子区间是否与询问的区间有重合部分,如果两者交集为空,那就不需要询问了。
下面给出示例代码:
1 | int segadd(int p, int l, int r) |
线段树的区间修改
区间修改和区间求和有着相同的思路。
我们这里以区间加为例。
还是之前的例子,如果我们想要给区间 $[2,8]$ 同时加上一个数会怎样?
让我们再来看一下这个图:

其中白色的区间是完全和我们询问没有任何关系的区间,黄色的区间是与我们询问的区间有交集,但是没有被新闻区间所包含的区间。
红色的区间和橙色的区间都被询问区间所包含,其中红色的区间是我们在区间求和的时候返回了值的区间,橙色的区间虽然被询问区间包含,但是我们没有访问到他们。
区间修改也是一样的思路。我们只需要将需要的区间修改即可,剩下的被询问区间包含的区间只需要标记一下就可以了。
这里需要用到懒标记的思想。
懒标记
懒标记的意思就是很懒的标记。我们用到它的时候才会将它兑现,否则他就在那里静静地待着就可以了。
我们考虑给结构体里面加上一个懒标记,就像这样:
1 | struct SegTree |
当某个区间有懒标记的时候,就意味着它的子树里面的所有区间都应该被修改,但是目前没有应用上。
但是拥有懒标记的区间的值在修改的时候已经被修改好了。
每一次我们递归询问子区间的时候,我们就需要将这个懒标记下传(如果有的话)。
我们需要一个pushdown函数来完成这件事。
我们这里仍然以区间加为例:
1 | void pushdown(int p) |
例题
Luogu P3372 【模板】线段树 1
参考代码:Luogu P3372
Luogu P3373 【模板】线段树 2
参考代码:Luogu P3373
扩展
标记永久化
我们可以尝试一个思路:不下传标记。
我们重新思考一下懒标记的意义。
懒标记代表的是,这个点的所有子区间都需要被这个标记更新他们的值。
于是我们就可以将标记放进函数里面,随着函数下传,到时候也可以起到更新值的作用。
这样的方法适用于不能pushdown的时候。
具体情况我也没有遇见过,据说是需要配合可持久化权值线段树(aka主席树)使用。
示例代码:
1 | ll segsum(int p, int l, int r, int tag) |
线段树上二分
想不到吧,线段树还能优化二分!
我们考虑这样一个问题:我们需要找到一个位置 $pos$,使得 $[1,pos]$ 这个区间内数字的和不小于 $val$。保证所有权值非负。
那么我们可以直接进行二分,这样每做一次的复杂度是 $O(\log^2 n)$ 的。
我们可以用线段树来优化这样的过程。
我们带着 $val$ 在线段树上搜索。
如果当前节点的左儿子的权值 $\geq val$,就带着 $val$ 继续跳到左儿子搜索;
如果当前节点的左儿子的权值 $< val$,就带着 $val-tr[tr[p].ls].val$ 继续跳到右儿子搜索。
动态开点线段树
有时候我们需要维护的下标区域非常广(比如说 $10^9$),但是真正有值的地方其实很少。
我们当然不可能为这个序列直接创建一棵完整的线段树,这样子会耗费我们大量的空间维护许多无用的数据。
比如说维护一个序列里面有多少个数字大于某个数,但是这个数列的值域是 $10^9$,但是数列长度最多只有 $10^5$。
我们当然不可能直接创建一个覆盖整个值域的线段树,这样子会需要我们创建 $2^31$ 个节点,即使我们不考虑区间修改,只维护一个区间和的话也需要高达24GiB的空间,十分的浪费。
于是我们可以动态开点,只建立用到的区间,其他的就不会被声明,大大减少了我们需要用的空间。
或者说,我们什么时候需要用到某个节点了,我们就建立它。
但是这样做的代价就是我们无法再使用简单的 p<<1 和 p<<1|1 来访问当前节点的左右子节点了。
我们需要记录下当前节点的左右节点的编号。
我们以维护一个序列里面有多少个数字大于某个数为例。
那么我们的结构体就会变成这个样子:
1 | struct SegTree |
其中 ls 和 rs 分别代表了当前节点的左儿子和右儿子的编号。
那么我们就不需要build了,只需要一开始将第一个节点初始化为根节点即可。
然后我们的区间修改函数就是这个样子的。
我们可以有两种风格:
我们在访问子节点之前,首先看一下我们将要访问的这个子节点到底是否存在,如果不存在的话就新开一个。
这样子的话支持把当前区间的左右端点放在结构体里面存着,也支持将区间左右端点当做参数放到函数里面传。
1 | void segadd(int p, int l, int r, int k) |
我们在访问子节点的时候才看一下,我们的这个子节点是否存在。如果不存在的话就创建一个。
这样的话我们就在函数里面传节点编号的引用,并且同时把当前区间的左右端点放进函数里面当参数传。
1 | void segadd(int &p, int l, int r, int al, int ar, int k) |
而查询函数不需要做太大的变动,只需要看一下当前访问的节点是否存在就可以了。
1 | int segsum(int p, int l, int r) |
可持久化权值线段树
面对眼前的区间第 $k$ 小问题,我们应该怎么办?
我们的一个思路就是使用主席树。
主席树,全称为可持久化权值线段树,通过保存每次插入操作时的历史版本,以便查询区间第 $k$ 小。
怎么保存呢?
一种暴力的方法就是可以每一次插入的时候都开一棵线段树。
但是这样对空间的使用不是很友好。
那么我们分析一下,每一次修改的时候涉及的都只有一条从根节点到我们想要修改的节点的路径。
那么我们每一次只需要新建从根节点一直到我们想要修改的节点的一整条路径就可以了。
我们每一次就只新建了 $O(\log n)$ 个节点,大大节省了我们需要用的空间。
这种情况下,我们就不能采用堆式存储法(就是那个把左儿子和右儿子分别设为 $p << 1$ 和 $p << 1 | 1$ 的)了,必须使用动态开点。
对于预计需要的节点个数,我们可以采用这种办法:
我们每一次操作最多需要新开 $2^{\lceil \log n \rceil +1}$ 个节点,我们只需要根据 $n$ 和 $m$ 的大小来声明就可以了。
怎么维护区间第 $k$ 小?
一般情况下,我们可以用对区间建立一棵权值线段树的方法来维护当前区间的区间第 $k$ 小。
原理就是,权值线段树维护的是区间内每一个数有多少个。
我们只需要用类似线段树上二分的思想在线段树上搜索即可。
但是我们不能每一次都根据当前区间建立一棵线段树,这样又麻烦又浪费空间。
所以我们就像利用前缀和减去另一个前缀和得到区间和一样,将给当前区间建立一棵线段树的问题转化成了给分别建立在 $[1,l-1]$ 和 $[1,r]$ 上的两棵线段树做差。
而这样的两棵线段树可以通过每一次向线段树维护的区间最后追加一个数字来得到。
而这也就是主席树维护区间第 $k$ 小的主要思想。
例题
Luogu P3834 【模板】可持久化线段树 2
参考代码:Luogu P3834
Luogu P3919 【模板】可持久化线段树 1(可持久化数组)
参考代码:Luogu P3919
区间最大子段和
区间最大子段和也可以使用线段树来维护。
我们考虑记录一下每一个区间内的最大前缀和、最大后缀和、最大子段和与区间和。
区间合并的时候这样合并:
- 最大前缀和:左儿子的最大前缀和与(右儿子的最大前缀和与左儿子的区间和之和)取最大值;
- 最大后缀和:右儿子的最大后缀和与(左儿子的最大前缀和与右儿子的区间和之和)取最大值;
- 最大子段和:左儿子的最大子段和、右儿子的最大子段和与(左儿子的最大后缀和与右儿子的最大前缀和之和)取最大值;
- 区间和:直接加。
写了个重载加号:
1 | struct SegTree |
然后查询函数就是这个样子的:
1 | SegTree query(int p, int l, int r) |
如果用线段树维护区间最大子段和的话还可以支持单点修改。
思路跟正常的单点修改一样。
1 | void modify(int p, int pos, int k) |
[SNOI2020] 区间和
暴力修改,不是正解。
能过官方数据,但是不能过Hack数据。
提交记录:
洛谷:题面;记录。
LibreOJ:题面;记录。
线段树优化建图
线段树优化建图,又称线段树优化连边,是一种处理区间连边的方法。
有时候题目会让我们从一个点 $w$ 向一段区间 $[l,r]$ 内的所有点连上一条边权相等的边。
连边数量少的时候我们尚且还可以通过枚举来暴力建边,而当连边数量多起来的时候时间复杂度就不符合我们的要求了。
我们可以利用线段树来辅助我们建图。
线段树上的每一个节点都是一个虚拟的节点,其分别向其左儿子和右儿子连接一条没有影响的边。
这里的“没有影响”不仅指边权为0,还可以指流量为 $+\infty$、费用为0等等。
网络流相关的题目中利用这种方式优化建图的很多。
建图的时候,我们首先建立线段树,建立 $2^{\lfloor \log{n} \rfloor +1}$ 个节点和 $2^{\lfloor \log{n} \rfloor +2}$ 条双向边。
然后就是处理区间连边问题。
我们就像正常的线段树区间加一样,函数递归时,如果遇到了被完全包含在询问区间内的第一个区间,就从我们指定的点向代表该区间的点连一条边并返回即可。
例题:
洛谷 P8021 [ONTAK2015] Bajtman i Okrągły Robin
如果我们使用暴力建图的话,可以想到的是把每一个 Robin 向他能抢劫的时间点连一条容量为1、费用为 $c_i$ 的边。同时,源点向每一个 Robin 连一条容量为1费用为0的边,每一个时间点向汇点连一条容量为1费用为0的边,然后跑最大费用最大流就可以了。
我们如果使用线段树建图的话,就仿照上面的方法,到线段树上连边就可以了。因为我们是在这一段区间内选一个时间点抢劫,所以我们连边的时候仍然保持上面的方式,容量为1、费用为 $c_i$。
题解:洛谷题解
参考代码:Luogu P8021