树链剖分

发表于 更新于 分类于 本文字数： 1579 阅读时长 ≈ 4 分钟

树链剖分。
Luogu P3384

引言

树链剖分（简称“树剖”，又称“重链剖分”）是一种将一棵树转化为一段连续的区间的方法。
这种方法可以将一棵树根据子树大小，也就是所谓的“重儿子”和“轻儿子”，来将一棵树划分成若干条”重链“，并可以保证，在任意一条路径上的连续的链都不超过 $\log_2{n}$ 个。

树剖可以借助一些数据结构（如线段树）来以 $O(\log n)$ 的复杂度维护数上路径的信息，如“修改树上两点之间的路径上所有点的值”和“查询树上两点之间的路径上节点权值的和/极值/其他(在序列上可以用数据结构维护的、便于合并的信息)”等等。

当然，除了上面那样做，树剖还可以快速地求LCA。

树剖在洛谷上有一道模板题：Luogu P3384
一道比较经典的例题：Luogu P2146 [NOI2015] 软件包管理器

思想

树剖的思想是，将一棵树按照“重边”来划分称为若干条“重链”。
当然，这里的“重链”只是指的一种常用的情况，其他的划分方法比如“长链剖分”等等就不在此赘述了。

重链

“重链”的定义是若干条首尾衔接的“重边”。
那么，如果想要了解“重链”，就需要先了解重边。

重边

“重边”的划分标准是它连接向一个重儿子。
这里需要注意的是，它只需要结束于一个重儿子，而无其他限制。
那么“重儿子”呢？

重儿子

“重儿子”是“重子节点”的别称。
我们判断一个子节点是否为重子节点的标准是它的子树大小。

对于一个节点的所有儿子，其中子树最大的那个儿子称为“重儿子”，其余的，则相对地称之为“轻儿子”。
连接某个节点和其重儿子的边叫做“重边”，而连接其与其轻儿子的边则相应地叫做“轻边”。

划分

我们首先看一下例子：

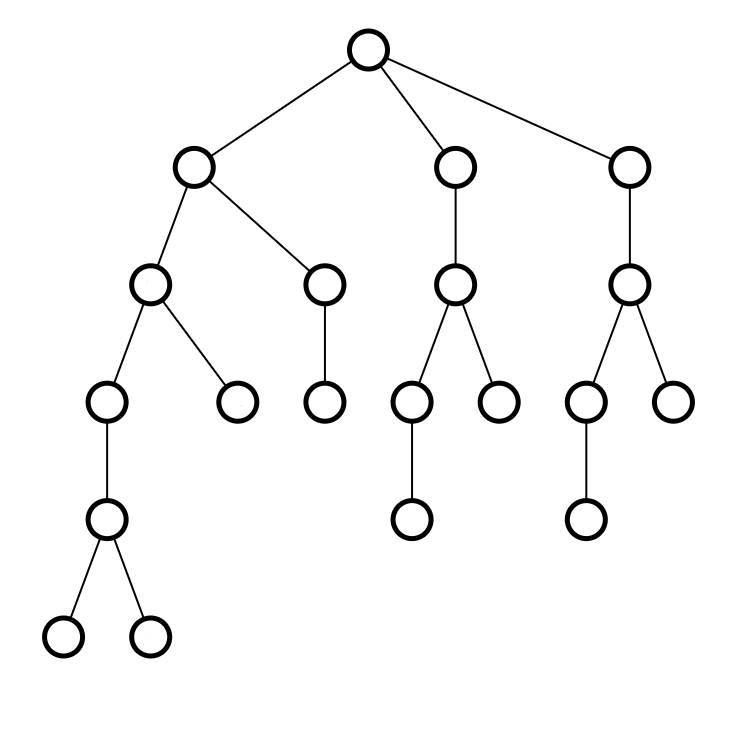
树剖1.png

这是一棵树。
对于上面的这一棵树，我们可以进行如下的一些标记：
我们首先按照深度进行分层：

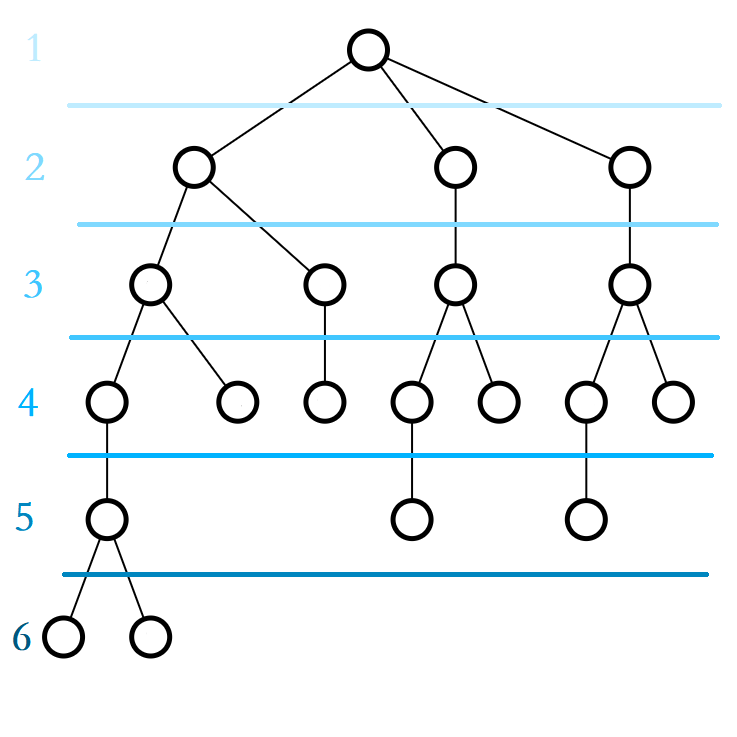
树剖2.png

然后标出子树的大小：

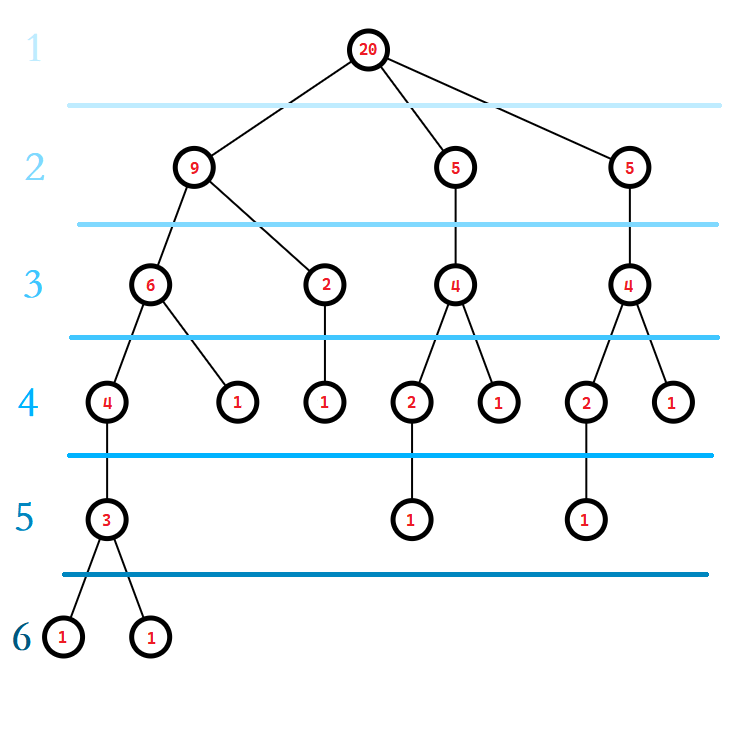
树剖3.png

然后标出轻儿子、重儿子、轻边和重边：

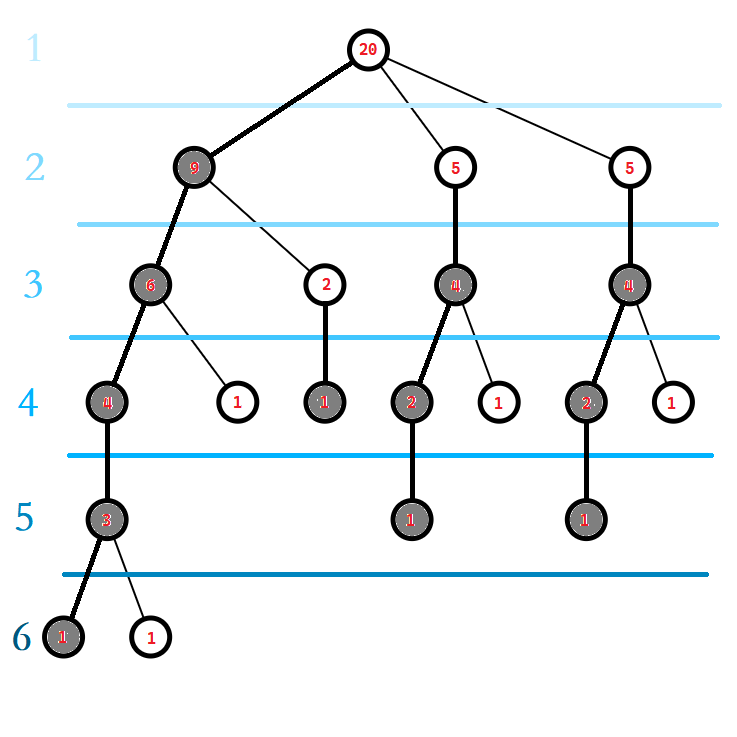
树剖4.png

然后标出重链：

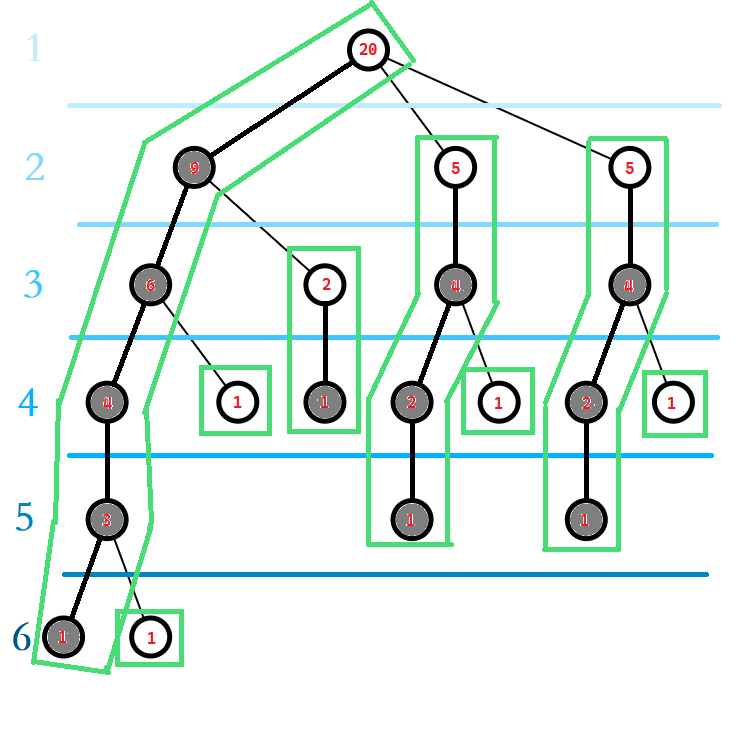
树剖5.png

最后标出DFS序：

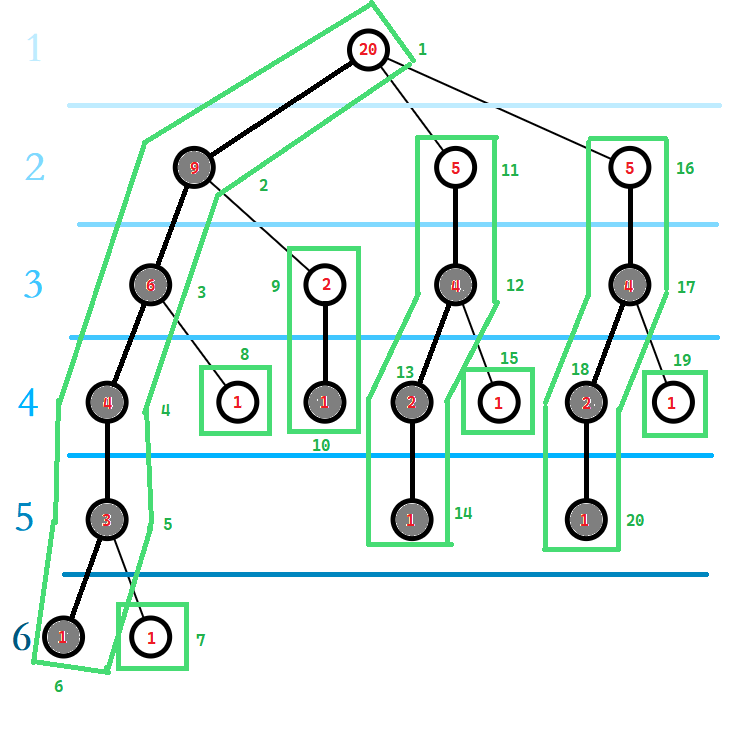
树剖6.png

这样就大功告成了。

实现

树剖的实现是通过两个DFS进行的。

我们这次使用邻接表来存储树的边信息：

1
2
3
4
5
6
int w[N], h[N], e[M], ne[M], idx;
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
    return
}

第一个DFS记录了每个节点的父节点(vater)、深度(depth)、子树大小(sz)和重儿子(son)：

1
2
3
4
5
6
7
8
9
10
11
12
13
void dfs1(int p, int fa, int depth)
{
    dep[p] = depth, ::fa[p] = fa, sz[p] = 1;//初始化节点状态，记录其深度和父节点
    for(int i = h[p]; ~i; i = ne[i])//遍历其所有儿子
    {
        int j = e[i];
        if(j == fa) continue;//防止遍历其父亲
        dfs1(j, p, depth + 1);//搜索当前儿子
        sz[p] += sz[j];//更新子树大小
        if(sz[son[p]] < sz[j]) son[p] = j;//判断是否为重儿子
    }
    return
}

第二个DFS记录了每个节点所在重链的链顶节点(top)、dfs序(id)和重新定向的节点权值(nw)：

1
2
3
4
5
6
7
8
9
10
11
12
13
void dfs2(int p, int t)
{
    id[p] = ++cnt, nw[cnt] = w[p], top[p] = t;//初始化节点信息，记录其DFS序
    if(!son[p]) return;//是否为叶节点
    dfs2(son[p], t);//优先搜索在同一条重链上的重儿子
    for(int i = h[p]; ~i; i = ne[i])
    {
        int j = e[i];
        if(j == fa[p] || j == son[p]) continue;
        dfs2(j, j);//搜索轻儿子，开一条新的重链，链顶为当前轻儿子
    }
    return
}

应用

树剖可以在 $O(n) \sim O(\log n)$ 的时间复杂度内求出两个点的LCA。

例题

板子题

洛谷上面提供了板子题。
题面见这里。
代码正确性见提交记录。

我们首先照常打出线段树部分（不会的可以看这篇博客各位读者们一定已经会线段树了罢）；
两个DFS也是已经有了的代码（见上面）；
然后就有了这篇代码的核心部分。

之后就是对题目要求功能的实现。

题目要求我们这样做：

  1. 将树从 x 到 y 结点最短路径上所有节点的值都加上 z。
  2. 求树从 x 到 y 结点最短路径上所有节点的值之和。
  3. 将以 x 为根节点的子树内所有节点值都加上 z。
  4. 求以 x 为根节点的子树内所有节点值之和。

我们分类型进行实现。

对于那些对某一棵子树进行的操作，我们直接调用线段树来进行操作，因为对于任意一棵子树，它里面的所有节点的DFS序就是连续的，也就意味着可以被当成一段区间来进行操作。

1
2
3
4
5
6
7
8
9
void addtree(int p, int k)
{
    segadd(1, id[p], id[p] + sz[p] - 1, k);
    return;
}
ll sumtree(int p)
{
    return segsum(1, id[p], id[p] + sz[p] - 1);
}

而对于路径的操作，我们使用这样一种策略：边走边计算。
首先，我们求出这一条最短路，也就是求出它们的最近公共祖先。
我们使用这样的思路来寻找他们的LCA：

我们从较深的那一个节点开始不断向上跳重链，直到跳到与较浅的节点同一条重链上为止。此时，深度较浅的那一个就是他们的LCA。

于是我们就可以写出路径加、路径求和的代码了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void addpath(int p, int q, int k)
{
    while(top[p] != top[q])
    {
        if(dep[top[p]] < dep[top[q]]) swap(p, q);
        segadd(1, id[top[p]], id[p], k);
        p = fa[top[p]];
    }
    if(dep[p] < dep[q]) swap(p, q);
    segadd(1, id[q], id[p], k);
    return;
}
ll sumpath(int p, int q)
{
    ll res = 0;
    while(top[p] != top[q])
    {
        if(dep[top[p]] < dep[top[q]]) swap(p, q);
        res += segsum(1, id[top[p]], id[p]);
        p = fa[top[p]];
    }
    if(dep[p] < dep[q]) swap(p, q);
    res += segsum(1, id[q], id[p]);
    return res % mod;
}

最后放一遍完整代码：Luogu P3384

[NOI2015] 软件包管理器

也是一道树剖的经典题目。

我们仔细想一下就可以知道，install操作可以将从当前节点到根节点的所有未安装的软件全部安装，而uninstall会将其子树内的所有软件一并卸载。

然后就是区间推平了。

详细的解释可以看我的题解。