快速求popcount和
一种以 $O(\log n)$ 的时间复杂度快速求 $\sum\limits_{i=1}^n \operatorname{popcount}(i)$ 的方法。
TL;DR
摆结论:
$$
\sum_{i=1}^n \operatorname{popcount}(i) = \sum_{i=1}^{\lceil \log_2(n) \rceil - 1} [(n>>(i-1)) \& 1==1] \times (i \times 2^{i-1} + 2^i \times \operatorname{popcount}(n>>i))
$$
其中 $[(n>>(i-1)) \& 1==1]$ 代表 $n$ 的第 $i$ 位是否为零。
原理
首先,我们可以想到一种 $O(1)$ 的求 $\sum\limits_{i=0}^{2^k-1} \operatorname{popcount}(i)$ 的方法。
这里以 $[0,2^5-1]$ 为例。
我们首先将所有数字列出来:
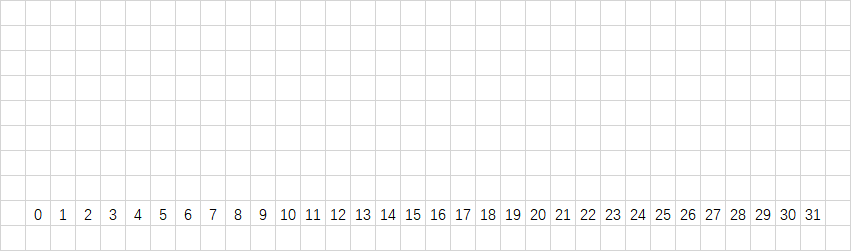
然后逐二进制位来看。
最低位的规律是01010101…:
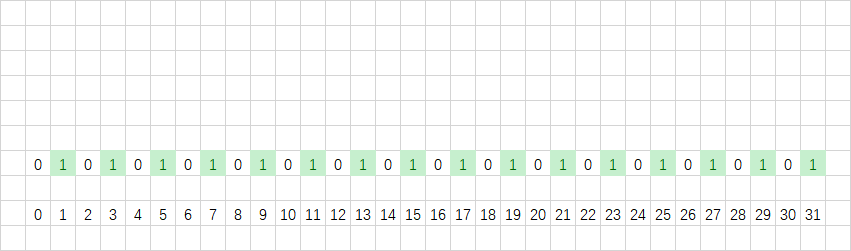
第二位的规律是00110011…:
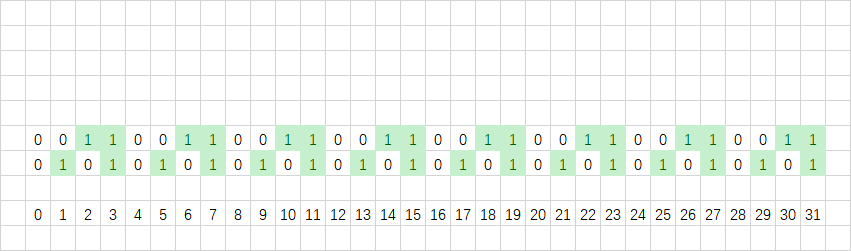
第三位的规律是00001111…:
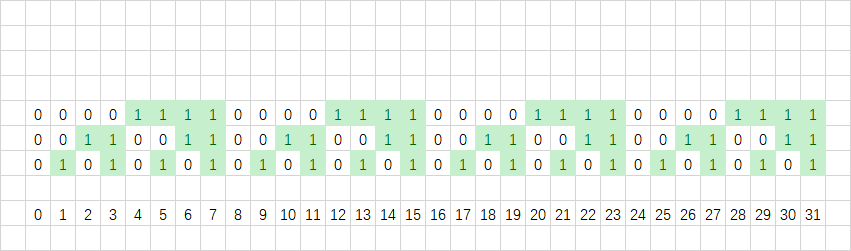
之后的规律也显然:
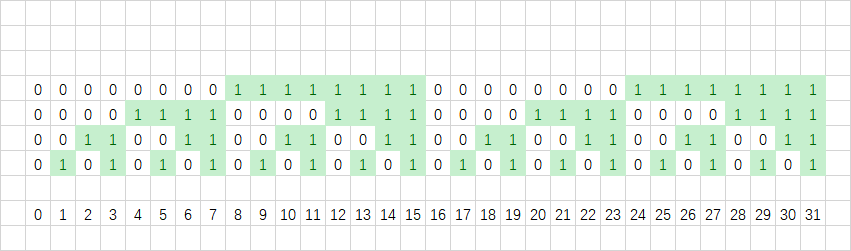
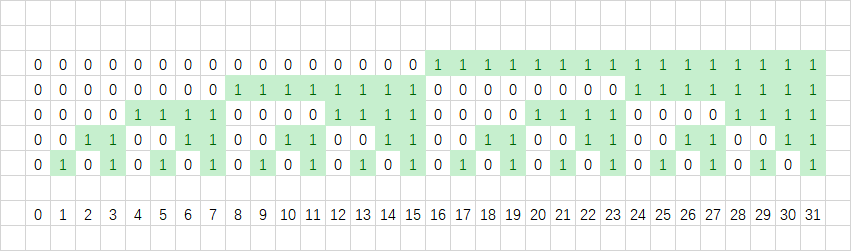
我们可以得到,每一位中都有一半是0,另一半是1。
于是我们就可以得出公式:
$$
\sum\limits_{i=0}^{2^k-1} \operatorname{popcount}(i) = k \times 2^{k-1}
$$
然后我们将给定的 $n$ 按照二进制位拆分。
这里以 $(11010110)_2 = (214)_{10}$ 为例。
(下面指的第几位都是从高向低数的)
其第一位是 $1$,所以我们可以向结果累加 $(00000000)_2 \sim (01111111)_2$ 的popcount和,也就是 $0 \times 2^7 + 7 \times 2^6$。
其第二位是 $1$,所以我们可以向结果累加 $(10000000)_2 \sim (10111111)_2$ 的popcount和,也就是 $1 \times 2^6 + 6 \times 2^5$。
其第三位是 $0$,对结果没有贡献。
其第四位是 $1$,所以我们可以向结果累加 $(11000000)_2 \sim (11001111)_2$ 的popcount和,也就是 $2 \times 2^4 + 4 \times 2^3$。
其第五位是 $0$,对结果没有贡献。
其第六位是 $1$,所以我们可以向结果累加 $(11010000)_2 \sim (11010011)_2$ 的popcount和,也就是 $3 \times 2^2 + 2 \times 2^1$。
其第七位是 $1$,所以我们可以向结果累加 $(11010100)_2 \sim (11010101)_2$ 的popcount和,也就是 $4 \times 2^1 + 1 \times 2^0$。
其第八位是 $0$,对结果没有贡献。
但其实不管有没有贡献我们都不算他了,因为我们只需要将 $[0,n)$ 这个区间分段即可。
最后再加上 $\operatorname{popcount}((11010110)_2) = 5$。
最终结果就是
$$
\begin{align}
& 0 \times 2^7 + 7 \times 2^6 + 1 \times 2^6 + 6 \times 2^5 + 2 \times 2^4 + 4 \times 2^3 + 3 \times 2^2 + 2 \times 2^1 \\ \notag
& + 4 \times 2^1 + 1 \times 2^0 + \operatorname{popcount}((11010110)_2) \\
={} & 448 + 256 + 64 + 16 + 9 + 5 \\
={} & 798
\end{align}
$$
因为 $\operatorname{popcount}(0) = 0$,所以统计上 $0$ 与不统计上其实没有本质上的区别。
代码实现
示例如下:
1 | scanf("%d", &n); |