博弈论(广义)学习笔记
简介: 博弈论
导入
我们先举一个栗子:
假如你和李zen一起玩一个游戏;
你们面前都有一个开关,你们都可以选择让这个开关处于断开或闭合两种状态的其中任意一种。
而我会根据开关的状态给你们评级:
当两个开关都闭合时,你们都得 $C$ ;
当两个开关都断开时,你们都得 $B$ ;
当两个开关一开一断时,断开的得 $D$ ,闭合的得 $A$ 。
十分简单。
你会怎么选呢?
首先我们列一个表格,表示出所有结果:
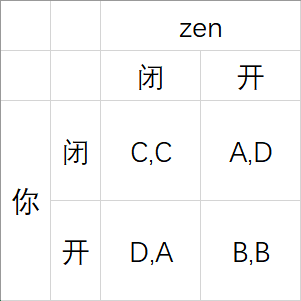
现在你会做出什么选择呢?
你犹豫了一下,然后闭合了开关。
毕竟这样你可以迫害李zen得到更高的评级。
但是你的内心深处还是有一个声音:
“断开开关吧,毕竟李zen之前被迫害太多次了,他会开始反围剿伤心的”
驱使着你断开开关。
是不是?
你仍然在犹豫。
那么,如果现在我们规定,本次游戏结果计入今年的期末考试,只有拿到 $C$ 级才能及格,而你又不想挂科,怎么样?
为了更直观一点,我们用 $[-1,2]$ 范围内的整数来代替评级,是不是会更好一些?
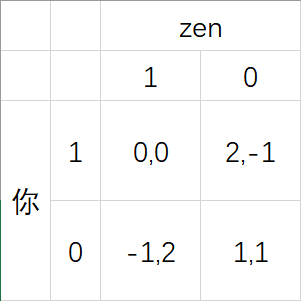
这时候,你就可以进行一下比较:
如果你闭合开关,那么无论李zen干什么,你都可以拿到更高的分数(除非他直接来找你) :
$0>-1,2>1$
此时,如果有两个策略 $α$ 与 $β$ ,无论他人选择什么,我们选 $α$ 得到的结果都严格优于选 $β$ ,那我们就称 $α$ 相对于 $β$ 是一个 严格优势策略(Strictly dominant strategy) 。
比如这道题里的“闭合开关”就是个相对于“断开开关”的严格优势策略。
假如你选择了断开开关,而李zen选择闭合开关,你挂科了。
这时候你就会得到一条重要的结论:
结论 1
永远,永远不要选择劣势策略。
这里的 “严格劣势策略(Strictly dominated strategy)” 是相对于 “严格优势策略” 而说的,指有一个策略,不管别人选择什么,你选它的结果都严格劣于选其他的策略。
懂的都懂。
所以说,你们两个人都选择断开开关,都得B,不是很好的吗?
这时候需要引入另一条重要的结论:
结论 2
理性的选择最终一定导致非最优结果。
对于zen来说,不管你怎么选,选择闭合开关总是对他有利的。但你不知道他会选什么,也不可以与它交流,所以你不能与他一起约好了选择断开开关。
现在,我们更改一下游戏的结果。
假如你考砸了,你就会受到家长的诘问,因而变得伤心,这一部分也要算在期望收益里;
假如你让李zen考砸了,你就会心生愧疚同时被愤怒的zen反围剿,也会变得伤心,这一部分也要算在期望收益里。
于是,我们的表格变成了:
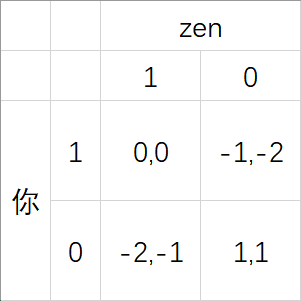
在这种情况下,你就不会有任何优势策略或劣势策略。
这个博弈叫做 “协和谬误(Coordination problem)” 。
这个时候你就不知道怎么办了。
你不知道李zen会怎么做,你们两个人也无法交流,因此你就无法做出决定。
这就引出了另外一条很好的结论:
结论 3
汝欲求之,必先知之。
你在做出决定之前,最好先了解一下你的对手的基本信息。
在这局游戏里,你的对手是李zen。
碰巧,你知道李zen富有爱心,他总会考虑你的感受。如果他闭合了开关但你没有而使得你输了,他会不开心的。
这就导致他之前和鳖玩的时候被邪恶的鳖打到自闭。(之前的不计入期末成绩awa)
你们两个会玩的十分愉快。(你输了他会安慰你awa)
但是如果你跟鳖玩呢?
鳖不会有情感损伤的减益よ。
那么,你的期望收益就变成了这样:
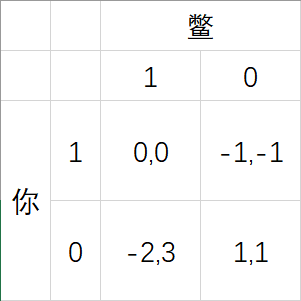
此时,你就需要对你的策略进行一些改变:
因为无论你选择什么,鳖总会闭合开关,因为这相对于他来说是一种优势策略。
所以,你应当闭合开关,使得鳖的收益最小。
这时候,你就学会了一条重要的结论:
结论 4
站在他人的立场上去分析他们会做出的决策 ,或者, 学会换位思考 。
现在,你大概就可以与鳖这样的人友好地游玩了,甚至能跟tue、zhua过上几招了。
但是,如果这个游戏的结果与你的期末考试成绩挂钩呢?
那么,就连zen也会闭合开关,来防止挂科的。
所以记住:
结论 5
人是自私的。人都想偷懒。
至此,你就基本上开始接触了博弈论。
大家应该都听说过囚徒困境罢。
不出意外的话,两个囚徒都会选择供出对方。
那么,如何改变这个博弈的结果呢?
如何改变博弈结果
我们有三种方法:
1. 签订条约,制定规章制度等;
2. 多次重复博弈;
3. 教育。(如集体主义教育)
不管哪一条,本质上都是改变了参与者的收益或参与者的动机。
更深的层次
我们刚才通过举例子知道了什么是博弈,但我们真的知道什么是博弈吗?
博弈的组成
一个博弈由三部分组成:
1. 参与人(Players)
在这里,我们使用小写字母 $i$ , $j$ 等来代表参与人。
2. 策略(Strategy)
在这里,我们使用带有下标的小写字母 $s_i$ 来代表参与人 $i$ 的某一个策略。
我们使用带有下标的大写字母 $S_i$ 来代表参与人 $i$ 的所有可能的策略集合。
我们使用小写字母 $s_{-i}$ 来表示除参与人 $i$ 之外的所有参与人的策略。
3. 收益(Payoff)
在这里,我们使用带有下标的大写字母 $U_i (s)$ 来代表参与人 $i$ 在所有参与者使用的策略为 $s$ 时所能得到的收益。(这一段好长啊)
另外的,我们使用小写字母 $s$ 来表示一个博弈。
好了,现在让我们来使用我们刚刚学会的表示方法来表示我们之前学过的东西。
那么,如果策略 $s_i$ 相对于策略 $s_i’$ 是一个严格优势策略的话,那么我们就可以写下
$$
\begin{equation}
U_i (s_i , s_{-i}) > U_i (s_i’ , s_{-i})
\end{equation}
$$
类似的,如果策略 $s_i$ 相对于策略 $s_i’$ 是一个严格劣势策略的话,那么我们就可以写下
$$
\begin{equation}
U_i (s_i , s_{-i}) < U_i (s_i’ , s_{-i})
\end{equation}
$$
弱优与弱劣
如果策略 $s_i$ 相对于策略 $s_i’$ 是一个严格优势策略,那么无论他人选择何种策略,那么我们选 $s_i$ 得到的结果都严格优于选 $s_i’$。
但有时候我们并不能总见到这样的策略。
那我们定义一个策略 $s_i$ 为相对于另一个策略 $s_i’$ 为 弱优策略(Weakly dominant strategy) ,此时只需要将大于号填上等于即可。
就像下面这样:
$$
\begin{equation}
U_i (s_i , s_{-i}) \leq U_i (s_i’ , s_{-i})
\end{equation}
$$
类似的, 弱劣策略(Weakly dominated strategy) 的定义如下:
$$
\begin{equation}
U_i (s_i , s_{-i}) \geq U_i (s_i’ , s_{-i})
\end{equation}
$$
所以说,对于刚才你和李zen做的游戏,我们可以用这些表示来替换之前的说法:
(先放图)

其中,
$S_{you} = \lbrace 1,0 \rbrace $
$S_{zen} = \lbrace 1,0 \rbrace $
$U_{you} (1,1) = 0 $
$U_{zen} (1,1) = 0 $
$U_{you} (1,0) = 2 $
$U_{zen} (1,0) = -1 $
$U_{you} (0,1) = -1 $
$U_{zen} (0,1) = 2 $
$U_{you} (0,0) = 1 $
$U_{zen} (0,0) = 1 $
$U_{zen} (1,s_{-zen}) > U_{zen} (0,s_{-zen}) $
$U_{you} (1,s_{-you}) > U_{you} (0,s_{-you}) $
现在你就可以理解刚才我们讲的符号是什么意思了。
迭代剔除劣势策略
让我们来做一个新的游戏。
你,李zen,鳖,tue,zhua,还有广大四班人民群众一起做一个游戏。每一个人都需要从范围为 $[1,100]$ 的整数里面选一个数。
AJ将会统计大家的结果,并进行总结。
总结后取平均数的 $\dfrac{2}{3}$ 作为基准数(向上取整)。基准数减去(你的结果与基准数的差)再除以基准数,得到一个百分数。这个百分数再乘以120就是你本次期末的数学成绩。
同时,AJ指定你和李zen为挑战对象。这意味着你如果比不过他,你就得承包他明年的巧克力供应了。
所以,你会选择哪一个数呢?
- 首先,你知道即使大家都选择100,基准数也是 $67\dfrac{1}{3}$ ,所以说选择67以上的数字是不明智的选择。
现在你把目光聚集到了 $[1,67]$ 范围内的整数上。
- 其次,即使大家都选择67,那么基准数也将会是 $44$ ,所以选择44以上的数字也是不太明智的选择。
现在你把目光聚集到了 $[1,44]$ 范围内的整数上。
- 然后,即使大家都选择了44,那么基准数也将会是 $28$ ,所以选择28以上的数字也是不很明智的选择。
……
最后,这个基准数字将会迭代到1。
不断剔除明显看起来劣势的策略,找出来此时新出现的劣势策略并予以剔除,这就叫 迭代剔除劣势策略(Iterative deletion of dominated strategies) 。
公共知识与相互知识
所以1是个明智的选择吗?
其实不是的。
大家都选择1的前提是,同学们都认为自己会选择1,且他人会选择1,且他人知道自己会选择1,且自己知道他人知道自己会选择1,且他人知道自己知道他人知道自己会选择1……
是不是绕起来了?
有一个相似的东西叫做 猜疑链 。
长度为2n+1的猜疑链大概是这样的:
你不知道我不知道你不知道我不知道你不知道……我不知道你不知道我不知道你在想什么。
省略的部分就不写出来了。
刚才我们遇见的东西看起来很像猜疑链,只不过“不知道”换成了“知道”。这就叫做 公共知识(Common knowledge) 。
但是在这个情况下,同学们们无法和对方沟通,无法知道别人的结果,所以这个东西是不能成立的。
AJ在统计完结果后让挑战对象互相看了对方的答案,但是你不知道李zen看了你的答案,同时李zen也不知道你看了他的答案。
这时候,公共知识的构建就停止在了某一层。这时候,我们就称其为 相互知识(Mutual knowledge) 。
是不是很简单?
中位选民定理
班长轮换时间到!
现在我们有两位班长候选人:bobo与武嘉。
而班级内将会产生十个不同的小团体,每个团体投一票。他们只会投给自己理想中的班长——也就是与自己交集最多的人。
小团体之间互无交集。
bobo和武嘉需要将自己定位到某一个小团体内,以计算选票。
现在我们将这些小团体分别命名为 $α,β,γ,δ,ε,ζ,η,θ,ι,κ$ 。
假如bobo选了η,而武嘉选了γ,那么他们两个人分别得到 $5.5$ 票与 $4.5$ 票。bobo会赢。
现在我们来模拟一下所有可能的结果。
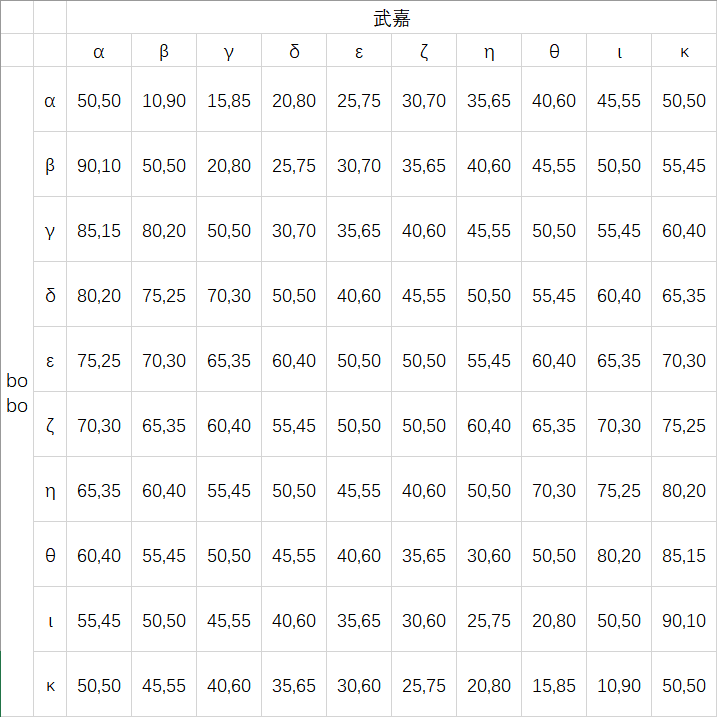
很明显,策略 $α$ 劣势于策略 $β$ ;去除策略 $α$ 后,策略 $β$ 劣势于策略 $γ$ ;去除策略 $β$ 后,策略 $γ$ 劣势于策略 $δ$ ;去除策略 $γ$ 后,策略 $δ$ 劣势于策略 $ε$ 。
同样的,策略 $κ$ 劣势于策略 $ι$ ;去除策略 $κ$ 后,策略 $ι$ 劣势于策略 $θ$ ;去除策略 $ι$ 后,策略 $θ$ 劣势于策略 $η$ ;去除策略 $θ$ 后,策略 $η$ 劣势于策略 $ζ$ 。
而策略 $ε$ 与策略 $ζ$ 没有优劣关系。
所以说,最后bobo和武嘉在进行玩迭代剔除劣势策略后,只能选择融入 $ε$ 和 $ζ$ 两个小团体之一了。
这就是著名的 中位选民定理(Median Voter Theorem) 了。
最佳对策与期望收益
现在让我们玩一个随机的游戏。
题面如下:
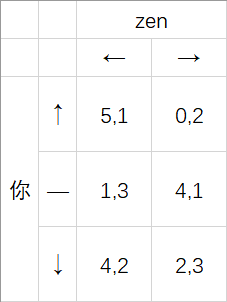
现在我们可以看到,没有明显的优势策略或劣势策略。
那我们该怎么办呢?
首先,我们可以看到,当李zen选择←时,选↑是我们的最佳对策;当李zen选择→时,选↓是我们的最佳对策。
但是你并不知道zen会选择什么。
你开始用AJ教你的数学知识来对每一个选项的期望收益进行一个模拟。
假设李zen选择←和→的几率是相等的,那么我们的期望收益如下:
$$
\begin{align}
U_{top} \ vs \ (\frac{1}{2} , \frac{1}{2} ) & = 5 \times \frac{1}{2} + 0 \times \frac{1}{2} = 2 \frac{1}{2} \\
U_{middle} \ vs \ (\frac{1}{2} , \frac{1}{2} ) & = 1 \times \frac{1}{2} + 4 \times \frac{1}{2} = 2 \frac{1}{2} \\
U_{down} \ vs \ (\frac{1}{2} , \frac{1}{2} ) & = 4 \times \frac{1}{2} + 2 \times \frac{1}{2} = 3
\end{align}
$$
此时我们可以看到,选择↓是我们的最佳对策(也是最安全的对策),因为 $2 \dfrac{1}{2} < 3 $ 。
但是如果你知道了李zen选择←或→的概率呢?
上图。
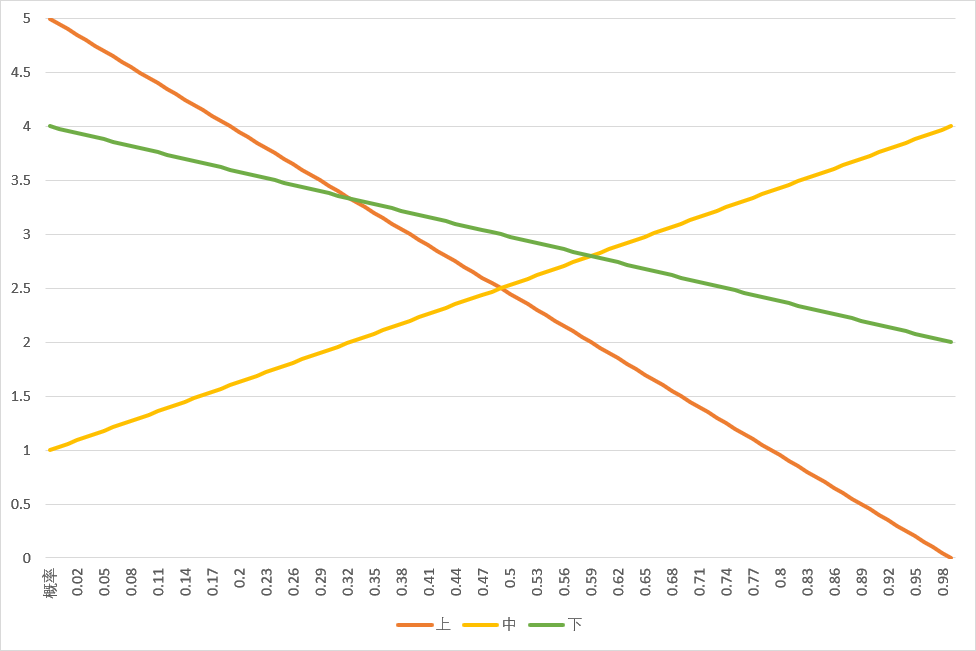
图中的横轴代表李zen选←的概率,同时选→的概率是(1-选←的概率)。纵轴代表不同选择的期望收益。
所以,我们可以看到,在李zen选择某一策略的概率不同时,我们的最佳对策是不一样的。
在这里,我们可以这样定义 最佳对策(Best Responce) :
当
$$
U_i ( \hat{s_i} ,s_{-i} ) \geq U_i ( s_i’ ,s_{-i} ) \quad (s_i’ \in S_i )
$$
或
$$
U_i ( \hat{s_i} ,s_{-i} ) = max( U_i ( S_i , s_{-i}))
$$
或
$$
EU_i ( \hat{s_i} ,p ) \geq max( EU_i ( s_i’ , p)) \quad (s_i’ \in S_i )
$$
时,我们称 $ \hat{s_i} $ 是策略 $s_{-i} $ 的最佳对策。
其中, $EU_i ( s_i , p ) $ 指的是策略 $s_i$ 在参与人 $i$ 持信念 $p$ 时的期望收益。
同时,我们需要注意一下,对于不同的策略集合 $s_{-i}$ ,其最佳对策的数量可能是不同的,且可能不为一(就是最佳对策不会只有一个)。
纳什均衡
定义
假设你需要和李zen一起完成一个项目。你将会付出 $s_y$ 个小时的时间,而zen将会付出 $s_z$ 个小时,其中 $s_y , s_z \in [0,10] $ 。
你们的收益为:
$$
\begin{align}
U_y & = 2 ( s_y + s_z + b s_y s_z ) - s_y^2 \\
U_z & = 2 ( s_y + s_z + b s_y s_z ) - s_z^2
\end{align}
$$
此时让我们来算一下我们怎么最大化我们的收益。
首先求一下导,把 $s_z$ 当做常数:
$$
\begin{align}
U_y’ & = 2 ( 1 + b s_z ) - 2 s_y \\
U_y’’ & = -2 < 0
\end{align}
$$
此时令 $U_y’ = 0 $ ,可以求出最佳对策:
$$
\begin{align}
2 ( 1 + b s_z ) - 2 s_y & = 0 \\
1 + b s_z & = s_y \\
s_y & = \frac{1}{1-b}
\end{align}
$$
此时画一下图:

此时我们可以看到,两个人的最佳对策函数交于了一点。
在实际情况中,因为你们两个都想偷懒,所以你们会不断剔除掉双方付出过多的策略,最终直到选择那个交点。
这个就叫做 纳什均衡(Nash Equilibrium) 。
其定义是:
对于一个已选对策的集合$ \lbrace s_1^* , s_2^* , s_3^* , \dots , s_m^* \rbrace $ ,其纳什均衡是满足下列条件的策略集合:
对于 $ \forall $ 参与人 $i$ 来说,其策略 $ s_i^* $ 是 $ s_{-i}^* $ 的最佳对策。
要实现纳什均衡,我们需要几个动机。
动机 1
人们永不反悔。
或者说,在所有人都已经选定好每个人的策略了之后,改变自己的策略并不会有额外收益。
动机 2
纳什均衡可以被看做一种自我实施的信念。
动机 3
tbc
找出博弈中的纳什均衡
假设我们现在与李zen玩一个新的游戏,题面如下:
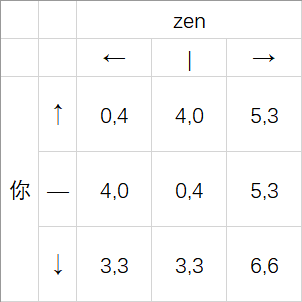
现在,我们用绿色的圆圈和红色的方框来分别表示你和李zen的最佳对策:
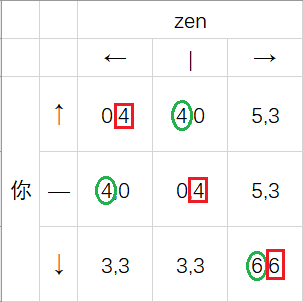
那么,这个博弈里的纳什均衡是什么呢?
我们可以看到,当你选择↓时,zen的最佳对策是选择→; 当李zen选择→时,你的最佳对策是选择↓。
一旦你们两个人中的其中一个选定了之后,另一个人就不会轻易跳出这个循环。
所以说, $(↓,→)$ 就是这场博弈里的纳什均衡。
当然,一场博弈的纳什均衡也可能不只有一个。
比如下图:
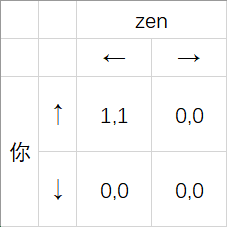
很简单是不是?
这时你们会发现,在这场博弈中,虽然看起来 $(←,↑)$ 明显是纳什均衡 (其实也真的是) ,但是如果你仔细看的话,右下角的那个零零也符合纳什均衡的定义,虽然两个人什么都得不到且傻子也会知道选择有收益的那个策略而不是一点收益都没有的,但是一旦两个人知道对方会选择这个零零,那就不会轻易更改自己的策略,不要忘了动机1、动机2和结论5。
这就类似全局最优解和局部最优解。
帕累托优势
在刚才上面那个博弈中,我们可以清楚的看到,左上的那个纳什均衡的收益是严格大于右下的那个的。
如果我们重复这次博弈。那么最终选择左上的几率会是百分之百。
这就叫做 帕累托优势(Pareto Dominate) 。
咕了。