傅里叶变换
简介: 傅里叶变换和FFT、复数、单位根
(20220321重修)
引入
今天AJ给大家留了一个作业:
多项式相乘。
$$
\begin{gather}
f(x) = (x^2 + 3x - 1) \\
g(x) = (2x^2 + x - 5) \\
f(x) \times g(x) = ?
\end{gather}
$$
大家都很认真、很用心地做了出来。
$$
\begin{align}
f(x) \times g(x) & = (x^2 + 3x - 1) (2x^2 + x - 5) \\
& = x^2 \times g(x) + 3x \times g(x) - g(x) \\
& = (2x^4 + x^3 - 5x^2) + (6x^3 + 3x^2 - 15x) + (2x^2 + x - 5) \\
& = 2x^4 + x^3 - 5x^2 + 6x^3 + 3x^2 - 15x + 2x^2 + x - 5 \\
& = 2x^4 + 7x^3 - 4x^2 - 16x + 5
\end{align}
$$
看起来很复杂,对吗?
但是,精通数学的王哥在纸上写写画画几十秒钟之后,得出来的答案跟正确答案也是一样的。
惊呆了的tüe问王哥他用的是什么办法。
王哥回答:“ 傅里叶变换 。”
多项式乘法的本质
王哥说:“我们知道,所有多项式都拥有如下的形式:
$$
f(x) = a_0 x^n + a_1 x^{n-1} + a_2 x^{n-2} + \cdots + a_{n-2} x^2 + a_{n-1} x +a_n
$$
我们也可以把一个多项式写成这样的形式:
$$
f(x) = \sum_{i=0}^n a_i x^{n-i}
$$
而两个多项式相乘 $f(x) \times g(x) = h(x)$ 的时候,相乘的结果的第 $k$ 项系数 $h_{k-1}$ 等于所有 $f_{i}$ 与 $g_{k-i}$ 乘积之和。
所以,
$$
h_k = \sum_{i=0}^{k-1} f_i \times g_{k-1-i}
$$
这样的方法算出的结果是与两个多项式的次数相关的。”
或者(对于OIer)通俗一点来说,假设两个多项式的次数分别为 $n$ 和 $m$,那么这个算法的时间复杂度是 $O(nm)$ 的。
给个模板题的44分代码:
1 |
|
$\color[rgb]{1,1,0.0625}{φ}$ (只保证44分)
DFT
多项式的点值表达
为了简便表达,我们使用 $f_k$ 来代表 多项式 $f(x)$ 的第 $k+1$ 项系数。
今天AJ的作业是昨天的延伸:
给定一个 $n$ 次多项式的 $n+1$ 个点值,要求我们求出这个多项式。
(还让武嘉给了样例,而武嘉给的样例是1,3,5,7,9,114514)
全班只有王哥和某盒子做了出来。广告:CoolHezi
他们用的是什么方法呢?
拉格朗日插值。
想要了解拉格朗日插值,可以参考我的这个博客:拉格朗日插值
现在我们只需要知道,给定了 $n+1$ 个任意点值,可以求出来经过这几个点的一个 $n$ 次多项式。
如果两个多项式 $f(x)$ 和 $g(x)$ 在相同纵坐标上取点(设其分别为 $f(x)$ 与 $g(x)$) 后相乘所得的结果($f(x) \times g(x)$)等于两函数相乘后对应纵坐标处的点值($h(x)$)。
举个栗子:
$$
\begin{align}
f(x) &= x^2 + 3x - 1 \\
g(x) &= 2x^2 + x -5
\end{align}
$$
我们分别取 $x \in [-1,1]$ 内的整数点所对应的点值:
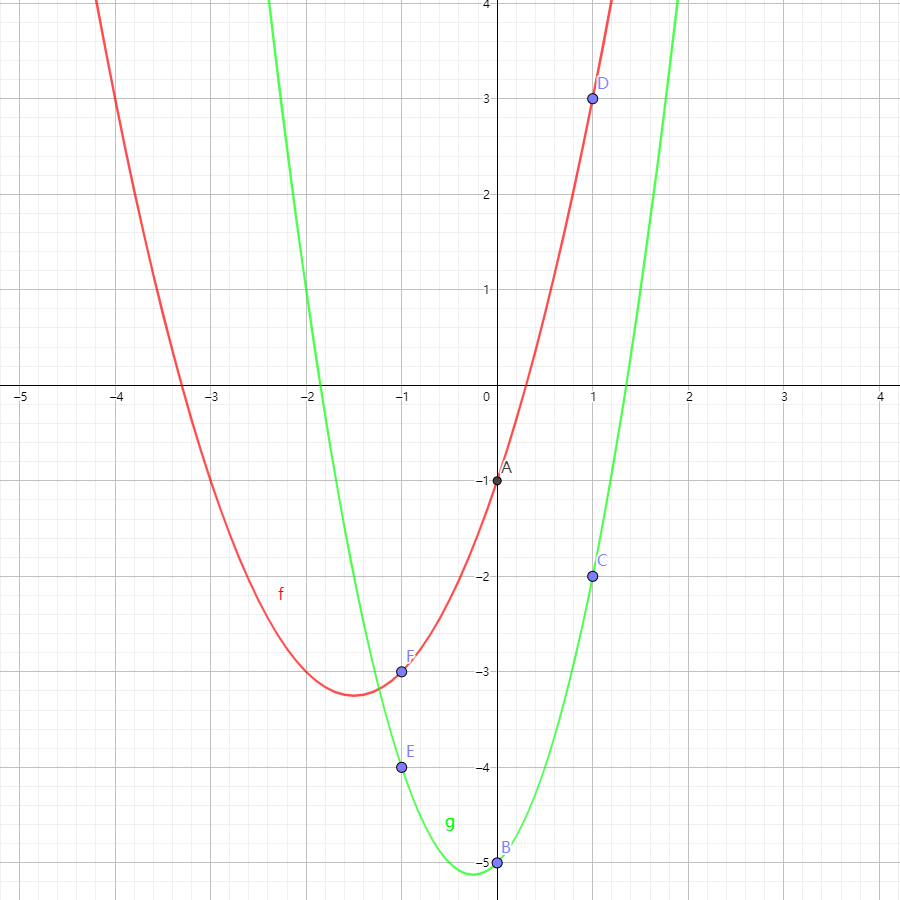
我们可以清楚的看到:
$$
\begin{align}
f(-1) & = -3 & f(0) & = -1 & f(1) & = 3 \\
g(-1) & = -4 & g(0) & = -5 & g(1) & = -2
\end{align}
$$
相乘之后可得:
$$
\begin{align}
h(-1) & = 12 & h(0) & = 5 & h(1) & = -6
\end{align}
$$
检验一下:

但想要求出 $h(x)$ ,我们至少需要4+1=5个点值。
怎么办?
多找几个啊。
于是我们就可以求出最终的多项式。
这就是FT的算法流程。
“把系数表达转换为点值表达”的算法叫做DFT
“把点值表达转换为系数表达”的算法叫做IDFT(DFT的逆运算)
P.S:
- 从一个多项式的系数表达确定其点值表达的过程称为求值(毕竟求点值表达的过程就是取了 n 个 x 然后扔进了多项式求了 n 个值出来);
- 而求值运算的逆运算(也就是从一个多项式的点值表达确定其系数表达)被称为插值。
F(Fourier)和T(Transform)有了,那F(Fast)呢?
单位根与复数
但是最终我们并没有觉得有什么可以加以利用的良好性质啊。
我们这些蒟蒻只会利用一些有理数和一些简单的无理数来进行一些简单的计算,再难一点的就不会了。
(而且这个多项式的次数和系数稍微一大就bz了)
准确来说,我们最终还是需要 $n+m$ 个点的求值与相乘,最终得到的时间复杂度与 $O(mn)$ 实际上差不太多,而且很可能在某些情况下更劣一些。
但是,法国数学家 傅里叶 横空出世,找了一些毒瘤数据代入,结果发现可以分治而使时间复杂度降低。
而他代入的正是单位根 $ω_{n+1}^{0 \to n}$ 。
复数
首先我们需要介绍复数。
已经会了的可以跳过。
(p.s.:下面我们使用的所有 $\sqrt{\quad}$ 标识都指的是平方根,算术平方根已使用+-来标记。)
复数的概念
虚数
我们所学的数轴是一条直线。

每一个有理数都能完美地与数轴上的某一个点一一对应。

$+\sqrt2$ 、 $+\sqrt3$ 等无理数也能很好地对应在数轴上。

但是人们说:“那 $+\sqrt{-1}$ 怎么办啊?”
我们找不到与 $+\sqrt{-1}$ 相对应的点。
而 $+\sqrt{-1}$ 又的的确确存在。
怎么办?
于是人们发明了一个概念:虚数。
而 $+\sqrt{-1}$ 在虚数里面叫做虚数单位,用 $i$ 表示。
所以,$i^2=-1$ 。
但是又有人会问:“那 $-\sqrt{-1}$ 又怎么办?”
用 $-i$ 呗。
但是在数轴上,人们仍然找不到对应虚数的点。数轴上的每一个点都对应了一个实数,没有办法找到任何一个新的点来对应虚数了。
所以,人们就在数轴的 0 处添加了一条新的数轴,来代表虚数。这条新的数轴垂直于代表实数的数轴,单位是 $i$ 。
复数及其运算
复数形似 $a+bi$ 。
其中 $a$ 称为实部( $\Re$ ), $b$ 称为虚部( $\Im $ )。
复数也有加减乘除等运算。
复数加减时实部虚部分别加减:
$$
(a+bi) \pm (c+di) = (a \pm c) + (b \pm d)i
$$
复数相乘时实部虚部分别相乘:
$$
\begin{align}
(a+bi) \times (c+di) & = a \times (c+di) + bi \times (c+di) \\
& = ac + adi + bci - bd \\
& = (ac - bd) + (ad + bc)i
\end{align}
$$
复数相除时就有点难办了。
直觉告诉我们 $\dfrac{a+bi}{c+di}$ 不会好化简。
这里需要引入一个概念:复数的共轭。
$a+bi$ 的共轭是 $a-bi$ 。
一个复数乘以其共轭最终得到的是一个实数。( $(a+bi) \times (a-bi) = a^2 + b^2$ )
所以当我们化简 $\dfrac{a+bi}{c+di}$ 的时候,我们只需要上下同乘分母的共轭就可以了:
$$
\begin{align}
\frac{a+bi}{c+di} & = \frac{(a+bi)(c-di)}{(c+di)(c-di)} \\
& = \frac{(ac+bd) + (bc-ad)i}{c^2+d^2} \\
& = \frac{ac+bd}{c^2+d^2} + \frac{bc-ad}{c^2+d^2} i
\end{align}
$$
复数在数轴上的表示
那我们怎么在数轴上表示复数呢?
之前我们说过了,虚数单位 $i$ 找不到一个合适的与其对应的数轴上的点。
那我们到底怎么办呢?
于是有人加了一条垂直于原本数轴的轴,用来表示复数的虚部。
就像这样:
于是我们举几个例子:

此时我们关注一下两个虚数的积:
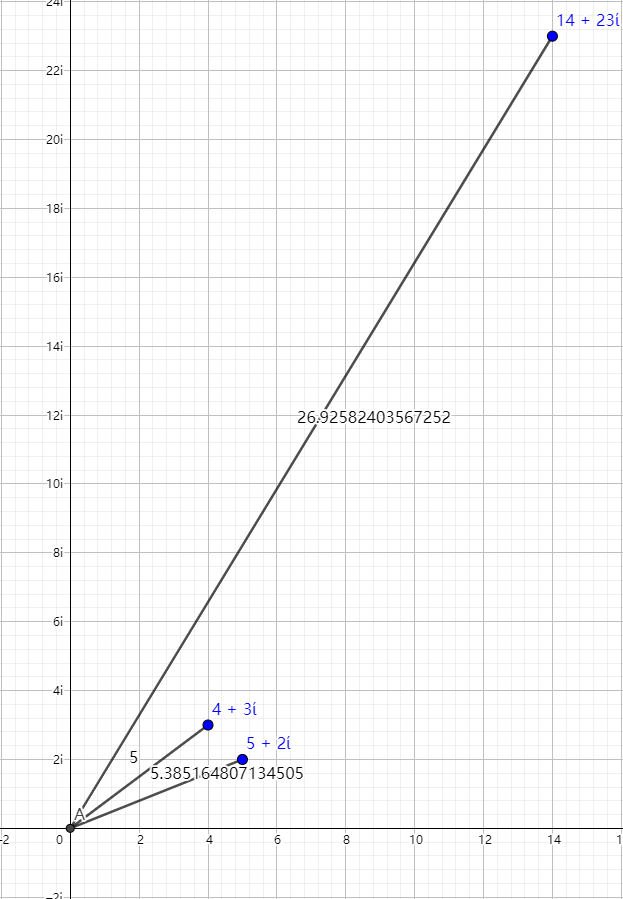
如果我们连接表示复数的点和原点,我们可以看见这三条线的长度分别是 $\sqrt{3^2+4^2}=\sqrt{25}=5$ ,$\sqrt{5^2+2^2}=\sqrt{29}$ 与 $\sqrt{14^2+23^2}=\sqrt{725} =5\sqrt{29}$ 。
凭借大家做几何题的直觉,我们可以看到, $5+2i$ 与 $x$ 轴的夹角与 $3+4i$ 与 $x$ 轴的夹角之和等于 $14+23i$ 与 $x$ 轴的夹角。
而且,通过刚才的例子,我们也可以看见 $5+2i$ 与原点的连线的长度与 $3+4i$ 与原点的连线的长度之积等于 $14+23i$ 与原点连线的长度。
数学家们为了简便地表示这些东西,发明了两个名词:幅角和模长。
所以,我们可以说,两个复数相乘时,幅角相加,模长相乘。
证明:
我们设三个点分别为 $A$ ,$B$ 与 $C$ 。

我们分别连接 $AO$ , $BO$ 与 $CO$ 。
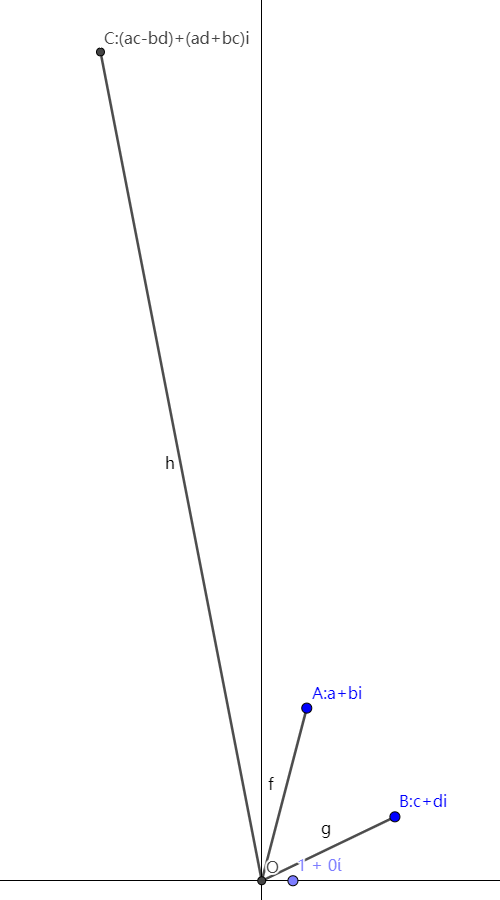
因为 $C$ 点代表的是 $(ac-bd)+(ad+bc)i$ ,所以 $AO$ , $BO$ 与 $CO$ 的长度分别是:
$$
\begin{align}
AO &= \sqrt{a^2 + b^2} \\
BO &= \sqrt{c^2 + d^2} \\
CO &= \sqrt{(ac - bd)^2 + (ad+bc)^2}
\end{align}
$$
我们化简一下 $CO$ 的表达式,可得:
$$
\begin{align}
CO & = \sqrt{(ac-bd)^2+(ad+bc)^2} \\
& = \sqrt{a^2 c^2 - 2abcd + b^2 d^2 + a^2 d^2 + 2abcd + b^2 c^2} \\
& = \sqrt{a^2 (c^2 + d^2) + b^2 (c^2 + d^2)} \\
& = \sqrt{(a^2 + b^2) (c^2 + d^2)} \\
& = \sqrt{a^2 + b^2} \times \sqrt{c^2 + d^2} \\
& = AO \times BO
\end{align}
$$
我们可以得出, $CO=AO \times BO$ 这一结论。
我们再连接 $BC$ 与 $AD$ ,$D$ 点代表 $1+0i$ 。

凭借你做几何题的直觉,你应该知道 $\triangle AOD$ 与 $\triangle COB$ 看上去是相似的。
没错,他们就是相似的。
证明:
我们先算出来 $AD$ 和 $BC$ 的模长:
$$
\begin{align}
AD & = \sqrt{(a-1)^2 + b^2} \\
BC & = \sqrt{(ac-bd-c)^2 + (ad+bc-d)^2} \\
& = \sqrt{[(a-1)c-bd]^2 +[(a-1)d + bc]^2} \\
& = \sqrt{(a-1)^2 c^2 - 2(a-1)bcd + b^2 d^2 + (a-1)^2 d^2 + 2(a-1)bcd + b^2 c^2} \\
& = \sqrt{(a-1)^2 (c^2 + d^2) + b^2 (c^2 + d^2)} \\
& = \sqrt{[(a-1)^2 + b^2] (c^2 + d^2)} \\
& = \sqrt{(a-1)^2 + b^2} \times \sqrt{c^2 + d^2} \\
& = AD \times BO
\end{align}
$$
接下来我们证明两三角形相似:
$$
\begin{gather}
\because
CO = AO \times BO , DO = 1 \\
\therefore \frac{CO}{AO} = \frac{BO}{DO} \\
\because BC = AD \times BO\\
\therefore \frac{BC}{AD} = BO \\
\therefore \frac{CO}{AO} = \frac{BO}{DO} = \frac{BC}{AD} \\
\therefore \triangle COB \sim \triangle AOD \\
\therefore \angle DOA = \angle BOC \\
\because \angle DOC = \angle DOB + \angle BOC \\
\therefore \angle DOC = \angle DOB + \angle DOA
\end{gather}
$$
证毕。
单位根
现在我们来介绍单位根。
单位根的意义是 $n$ 次方为 1 的复数,也就是 $x^n=1$ 的复数解。
如果你学过三角函数的话你应该十分清楚什么是单位圆。
而单位圆可以帮我们更好地理解什么是单位根和单位根为什么能够代入之后能实现分治。
我们先画出一个单位圆:
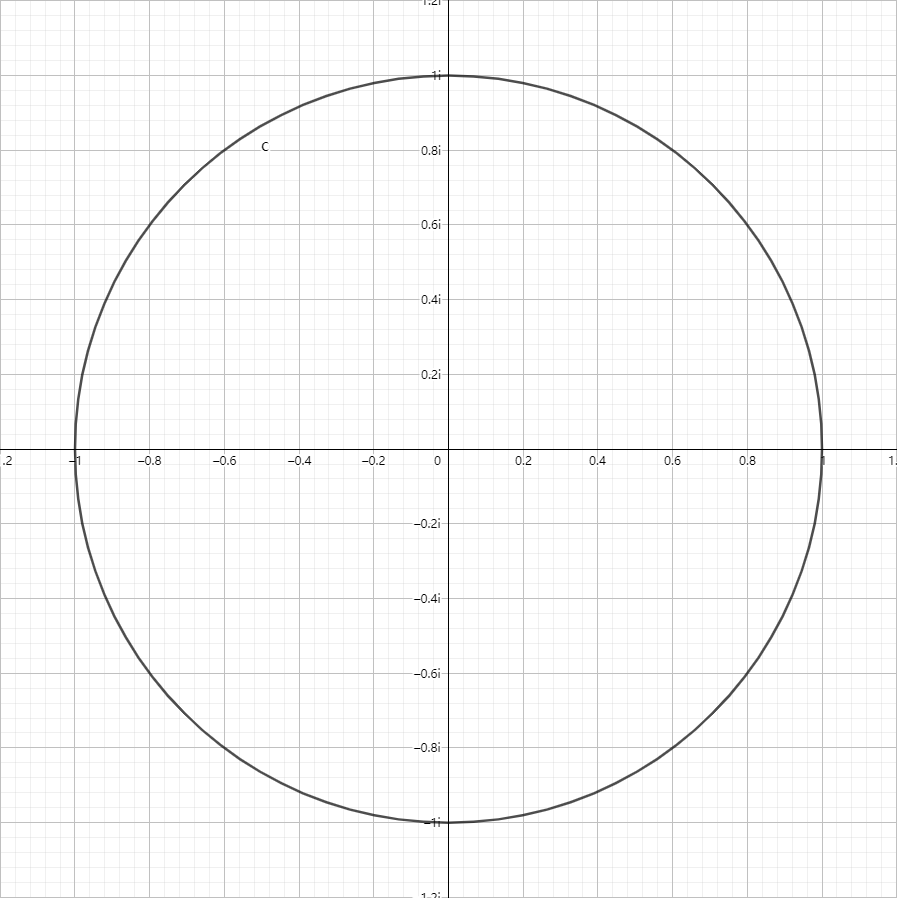
我们知道, $1^n=1$ ,所以单位根的其中一个一定是 $1$ 。
我们连接 $1$ 和 $0$ 。
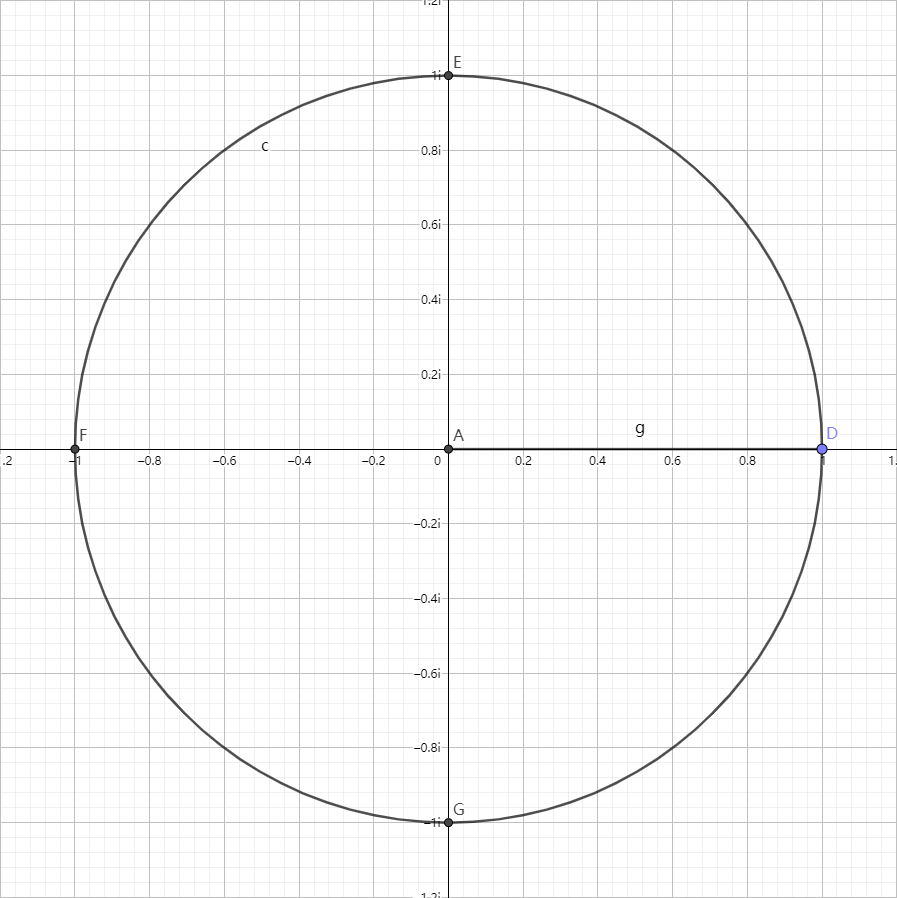
我们在这里举一个 $n=4$ 的栗子来帮助我们理解单位根。
首先,我们知道, $(\pm i)^2 = -1$ ,而 $-1^2=1$ ,
所以 $i$ 和 $-i$ 也是 $n=4$ 时的两个单位根。
当然,因为 $(-1)^2=1$ ,所以我们不能丢下-1。
至此,我们就找齐了 $n=4$ 时的所有单位根。
我们记单位根分别为 $ω^0_4 , ω^1_4 , ω^2_4 , ω^3_4$ 。
但哪个对应哪个呢?
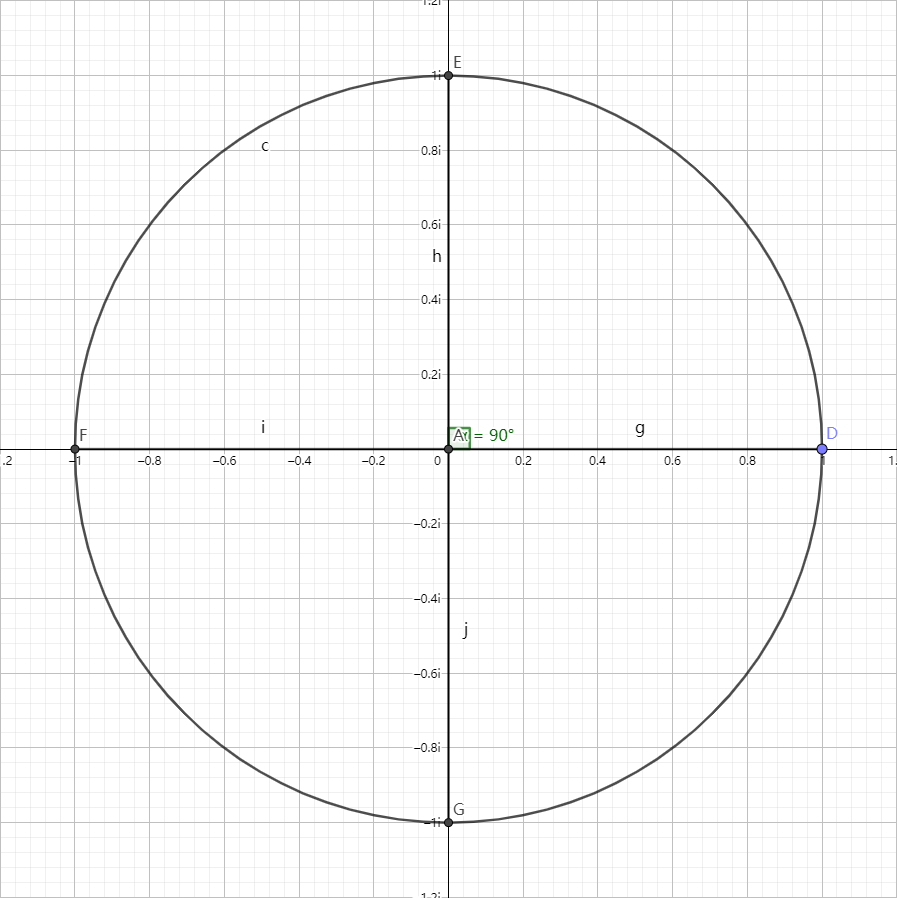
当我们观察图像的时候,我们可以发现这四个点与原点的连线可以平分这一个单位圆。
每相邻两条线之间的夹角都是 $90^{\circ}$ 。
当我们推广到 $n=8$ 的时候。我们可以另外得到 $\frac{1}{\sqrt2}+\frac{1}{\sqrt2}i , \frac{1}{\sqrt2}-\frac{1}{\sqrt2}i , -\frac{1}{\sqrt2}+\frac{1}{\sqrt2}i , -\frac{1}{\sqrt2}-\frac{1}{\sqrt2}i$ 四个单位根。
我们把他们表示在复平面上之后会是这样一个情况:
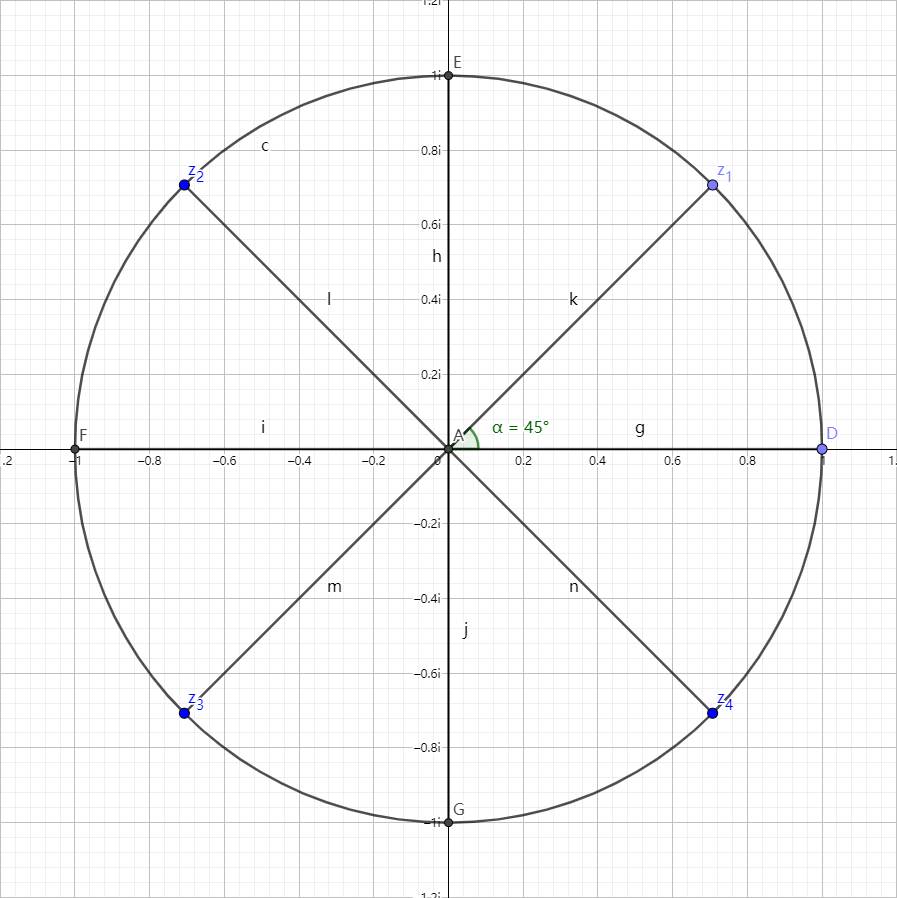
我们会发现,新增的这四个单位根所对应的点也在圆上,且所有的这几个点与圆心\原点的连线平分这个单位圆为8份。
所以我们可以这样理解,所有的 $ω_n^{0 \to n-1}$ 与原点的连线可以平分单位圆为 $n$ 份,且每相邻两条线之间的夹角都是 $\frac{2π}{n}$ (即 $\frac{360}{n}^{\circ}$ )
这样就好编号了:从 $1$ 开始,逆时针编号。
举个栗子:
$ω_8^{0 \to 7}$ 的值分别为 $1 , \frac{1}{\sqrt2} + \frac{1}{\sqrt2}i , i , -\frac{1}{\sqrt2} + \frac{1}{\sqrt2}i , -1 , -\frac{1}{\sqrt2} - \frac{1}{\sqrt2}i , -i , \frac{1}{\sqrt2} - \frac{1}{\sqrt2}$ 。
p.s.:虽然我们只承认 $ω_n^k$ 中的 $0\leq k < n$ 的情况,但是 $k\geq n$ 和 $k<0$ 的情况还是有的,这就跟 $\geq 2π$ (即 $360^{\circ}$ )和 $<0$ (即 $0^{\circ}$ )的角一样。
单位根的性质
单位根有很多性质,这里会列举几个。其中,最后一个是最重要的,也是我们选择代入单位根的原因。
- $ω^a_n + ω^b_n = ω_n^{a+b}$
可以从把单位根类比成切蛋糕的方法去理解。
- $(ω^1_n)^k = ω^k_n$
可以理解成把 $k$ 块蛋糕拼起来。
- $ω_{λn}^{λk} = ω_n^k$
同可以理解成把一块蛋糕平均切成 $\lambda$ 块。
- $ω^k_{2n} = - ω_{2n}^{(k+n)\bmod{n}}$
这是最重要的一条。
这条的证明可以在复平面上清晰的看出。
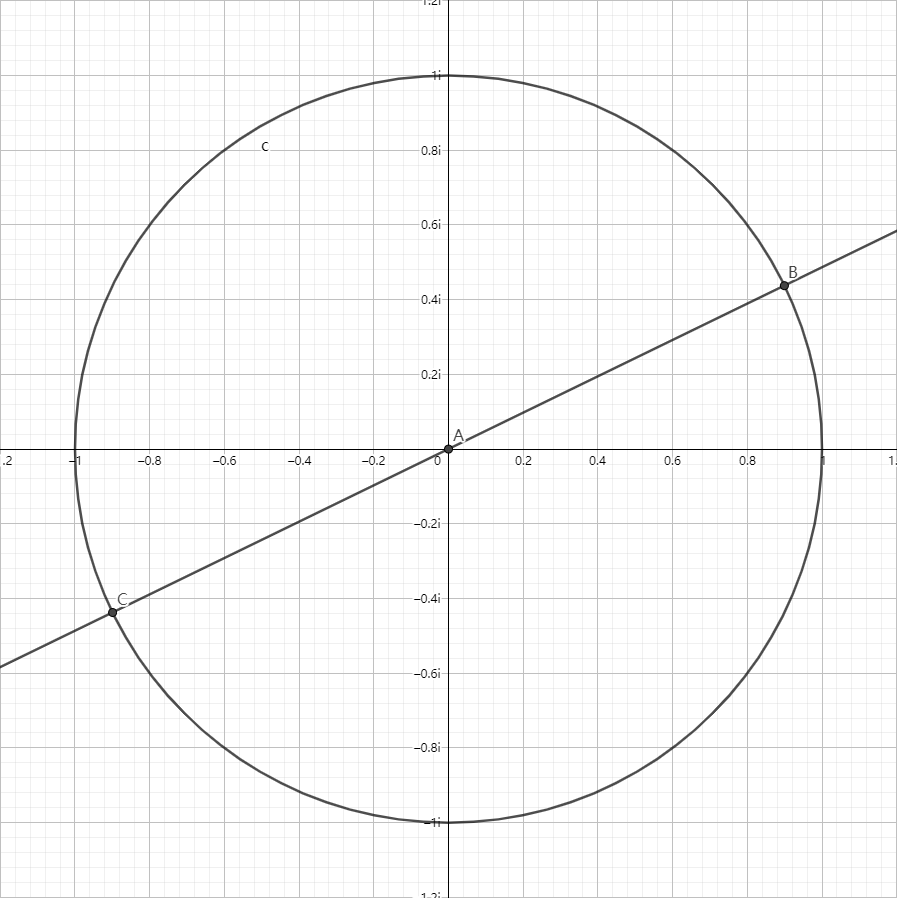
这一条性质是我们选择代入单位根的原因。但为什么呢?
FFT
分治
傅里叶把多项式 $f(x)$ 按照次数分成奇偶两部分。(忘了的向前翻再看一遍)
即,
$$
\begin{align}
f(x) &= \sum^n_{i=0} a_i x^{n-i} \\
&= \sum_{i=0}^{\frac{n}{2}} a_i x^{n-2i} + \sum_{i=0}^{\frac{n}{2}} a_{i+1} x^{n-2i-1}
\end{align}
$$
我们称 $\displaystyle \sum_{i=0}^{\frac{n}{2}} a_{i+1} x^{n-2i-1}$ 为 $f_o(x)$ , 称 $\displaystyle \sum_{i=0}^{\frac{n}{2}} a_i x^{n-2i}$ 为 $f_e(x)$ 。
此时我们把式子化简一下,可得
$$
f(x) = f_e(x^2) + x f_o(x^2)
$$
所以,我们想要计算 $f(x)$ 的话,只需要计算 $f_e(x)$ 与 $f_o(x)$ 即可。
当然,我们计算 $f_e(x)$ 与 $f_o(x)$ 的时候,也像刚才我们分解 $f(x)$ 一样,把它们分解掉。
最终我们可以达到分治的效果。
而我们不可能对于所有的点都进行实际的代入求值运算,那样会爆精度。
代入求值
我们刚刚介绍了单位根的性质,所以我们可以代入单位根来简化运算。
怎么简化?
我们尝试过代入几个整数来求值,但是那样子复杂度会爆掉。
然后我们就想到了代入相反数。
这样的话,我们只需要求出一半的值,就可以得到另外的所有值了。
我们还可以再快,即进行分治。
但是,分治要求我们每一次分治代入的值都为相反数,这要求了一对相反数的平方仍为相反数。
于是我们就找到了单位根。
我们代入 $ω^k_n$ ($0 \leq k < \dfrac{n}{2}$),可得:
$$
\begin{align}
f(ω^k_n) &= f_e((ω^k_n)^2) + ω^k_n f_o((ω^k_n)^2) \\
&= f_e (ω^k_{\frac{n}{2}}) + ω^k_n f_o(ω^k_{\frac{n}{2}})
\end{align}
$$
此时我们对这个式子进行稍稍的变动,可得:
$$
\begin{align}
f(ω^k_n) &= f_e((ω^k_n)^2) + ω^k_n f_o((ω^k_n)^2) \\
f(ω_n^{k+\frac{n}{2}}) &= f_e((ω_n^{k+\frac{n}{2}})^2) + ω_n^{k+\frac{n}{2}} f_o((ω_n^{k+\frac{n}{2}})^2) \\
&= f_e (ω_n^{2k+n}) + ω_n^{k+\frac{n}{2}} f_o(ω_n^{2k+n}) \\
&= f_e (ω_n^{2k}) + ω_n^{k+\frac{n}{2}} f_o(ω_n^{2k}) \\
&= f_e (ω_{\frac{n}{2}}^k) + ω_n^{k+\frac{n}{2}} f_o(ω_{\frac{n}{2}}^k) \\
&= f_e (ω_{\frac{n}{2}}^k) - ω^k_n f_o(ω_{\frac{n}{2}}^k)
\end{align}
$$
通过 $\begin{cases} f(ω_n^k)=f_e(ω_{\frac{n}{2}}^k)+ω^k_nf_o(ω_{\frac{n}{2}}^k) \\ f(ω_n^{k+\frac{n}{2}})=f_e (ω_{\frac{n}{2}}^k) - ω_n^k f_o(ω_{\frac{n}{2}}^k)\end{cases}$ 这两个式子,我们理论上是可以求出所有点值的。因为 $f_e(x)$ 与 $f_o(x)$ 理论上只有 $f(x)$ 次数的一半,只能得到完整地求出 $f(x)$ 所需要的点值的一半。而两个式子分别能求出一半且互不重复,合起来就是我们所需要的所有点值了。
但是当我们遇到某一层的 $f(x)$ 是奇数次的时候,我们应该怎么办呢?
答案是:自己补。
我们可以手动为这个多项式补成2的整数次幂次。当然,是在不影响多项式整体的值得前提下,所以我们选择补0,即我们补上去的所有的 $a_k$ 都是0。
代码实现
DFT
复数结构体
为了表示方便,我们使用结构体来表示复数。
我们同时重载一下运算符,以便做复数之间的四则运算。
1 |
|
$\color[rgb]{1,1,0.0625}{φ}$
预处理单位根
我们之前应该提到过什么是单位根。但是怎么快速求出我们需要用的所有单位根呢?
开根号的方法太慢了,打表又太难。
所以我们使用三角函数。
没学过三角函数的可以自己先学一下(话说为什么你会先学傅里叶变换?)
我们首先求出 $ω^1_n$ 。
[anime here]
C++的三角函数采用的是弧度制。而刚才我们已经介绍过什么是弧度了。
所以, $ω^1_n$ 就等于 $\cos(\dfrac{2π}{n})+\sin(\dfrac{2π}{n})i$ 。
把得到的结果依次乘起来就是所有的单位根。
1 |
|
$\blacktriangleright$
递归实现
1 |
|
$\blacktriangleright$
好了,我相信你已经学会了利用DFT把多项式拆成一系列点值了。
但是我们怎么把这些点值还原为多项式呢?
IDFT
IDFT只需要改变DFT中的一点东西就可以得到。
因为我们代入的时候,得到了一个点值序列,我们在此称其为 $u$ ,而 $\displaystyle u[k]=\sum_{i=0}^{n-1} (ω^k_n)^i f(i)$ ,所以 $\displaystyle f(i) = \frac{\sum\limits_{i=0}^{n-1} (ω_n^{-k})^i u[i]}{n}$ 。
具体的证明过程目前请见这里 。这个证明涉及到了单位根反演,可以再写一篇博客,所以我等写到的时候再补全证明。
上代码:
1 |
|
$\blacktriangleright$