Splay.
(2022 年 5 月 24 日重构)
Splay 是一种很好地维护一棵二叉搜索树的方法。
如果不知道什么是二叉搜索树,请看此页面。
基本函数
Splay 的基本思想是,通过一系列的旋转操作,维持整棵二叉搜索树的平衡。
首先,我们假设我们需要维护的结构体是这个样子的:
1
2
3
4
5
6
7
8
9
10
11
| struct Node
{
int s[2], fa;
int v, w;
int sz;
void init(int _v, int _fa)
{
v = _v, fa = _fa;
sz = w = 1;
}
}tr[N];
|
解释:
s[2]:左右子树。fa:父亲。v:节点权值。w:节点大小。sz:节点及其子树大小。
还有一些其他的东西就一一列举了,比如懒标记等等。
旋转
Splay 之所以能够维持其平衡,依赖的就是这样的简单旋转操作。
左旋与右旋
对于这样一个图:
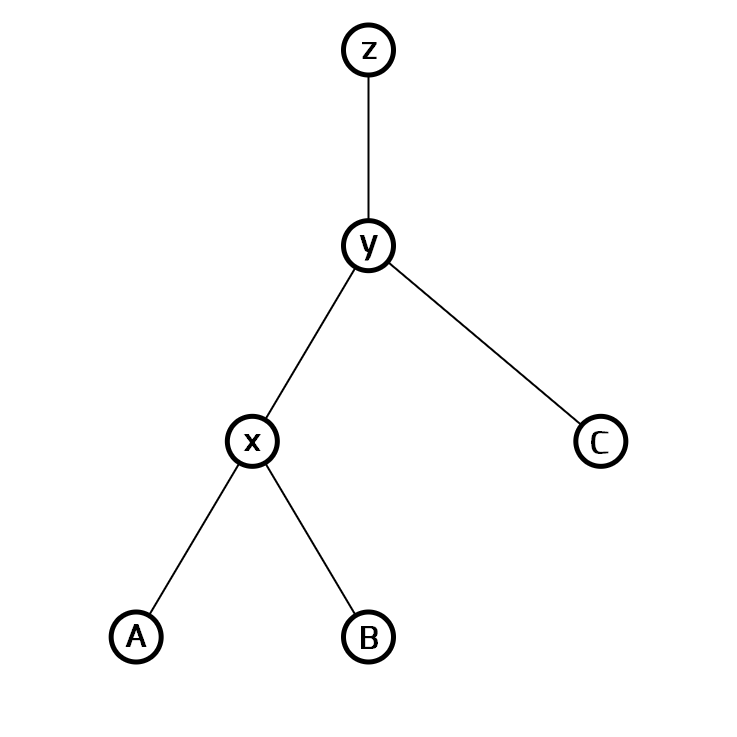
其中 x 节点有两个子树,A 与 B;x 节点的父亲 y 节点还有一棵子树 C;z 节点是 y 节点的父亲。
我们将 x 节点旋转(这里 x 节点是其父亲 y 节点的左儿子,所以我们会将其右旋),结果是这个样子的:
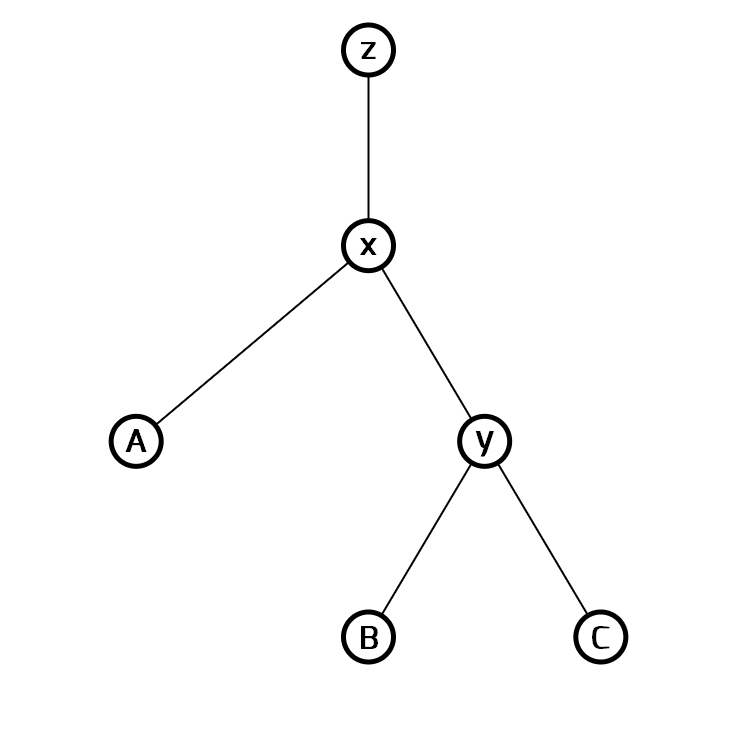
当然,如果我们把 x 旋转回去的话,那就是左旋操作了。
总体来看是这个样子:
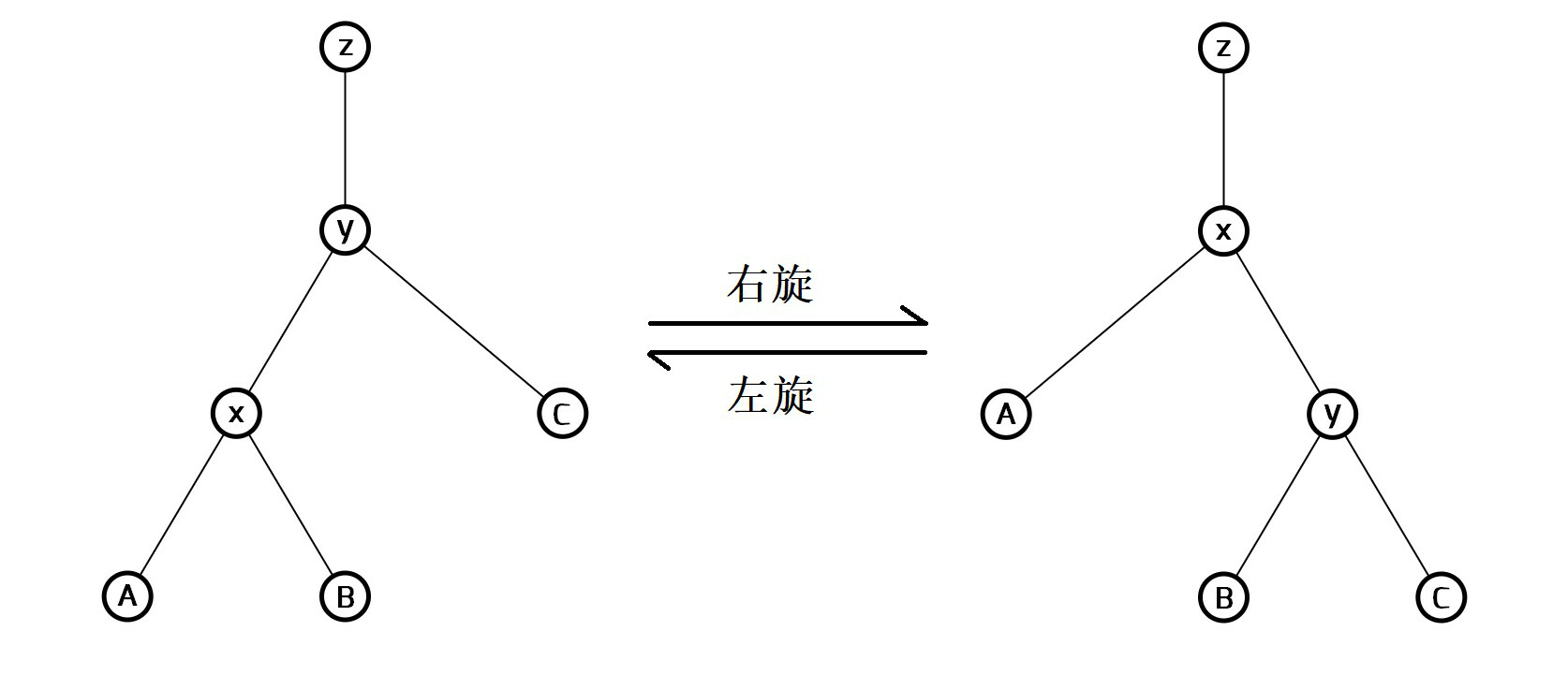
在进行旋转操作时,我们需要保持其中序遍历序列不变。
在刚刚的右旋操作中,我们来分析一下我们需要改变的边:
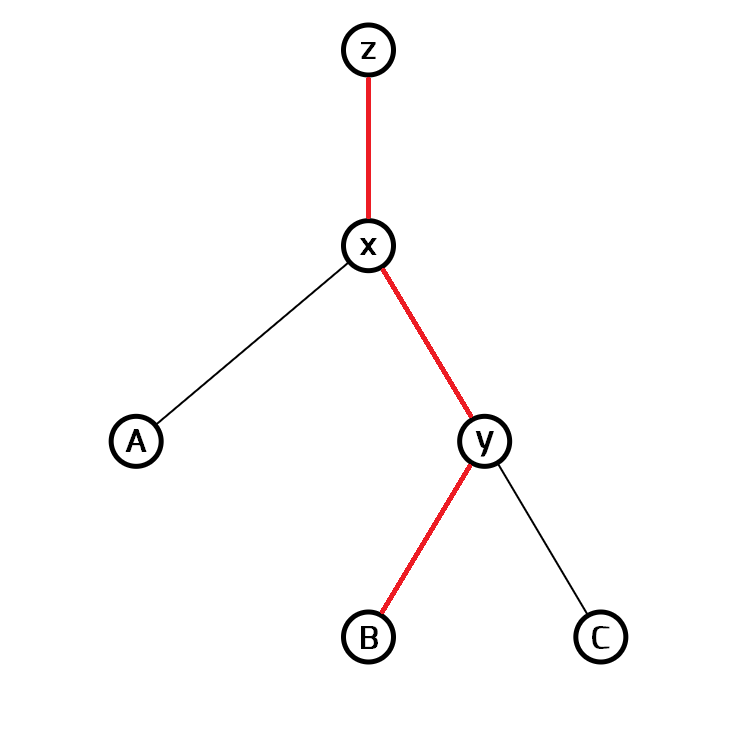
就是这三条标红的边。
那么对于这三条边,我们分别进行重构操作。
代码如下:
1
2
3
4
| int k = tr[y].s[1] == x;
tr[z].s[tr[z].s[1] == y] = x, tr[x].fa = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].fa = y;
tr[x].s[k ^ 1] = y, tr[y].fa = x;
|
旋转完成之后,因为我们改变了树的结构,所以我们需要重新计算 x 和 y 的大小,有时候还有需要维护的其他信息。
注意这里需要先维护较低的 y,再维护较高的 x。
所以总的函数是这个样子的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void pushup(int p)
{
tr[p].sz = tr[p].w;
if(tr[p].s[0])tr[p].sz += tr[tr[p].s[0]].sz;
if(tr[p].s[1])tr[p].sz += tr[tr[p].s[1]].sz;
}
void rotate(int x)
{
int y = tr[x].fa, z = tr[y].fa;
int k = tr[y].s[1] == x;
tr[z].s[tr[z].s[1] == y] = x, tr[x].fa = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].fa = y;
tr[x].s[k ^ 1] = y, tr[y].fa = x;
pushup(y), pushup(x);
}
|
核心函数
我们在向 splay 中插入一个数之后,会强制将其旋转到根。
而在刚才的示例中,我们看到了,我们将 x 右旋之后,x 就向上走了一点。
而经过不断的旋转,我们就可以让 x 节点走到根。
当然,我们也不是随便瞎转,因为旋转操作也是需要复杂度的。
而我们的最后目标是使之均摊之后达到尽量小的复杂度。
引用闫学灿的一句话:
“如果我们瞎转的话,就达不到 的复杂度了。”
所以我们要根据 x 所处的位置来制定不同的旋转方案。
首先,我们对于 x 可能出现的几种情况分析一下:
x 就是目标节点。
那么就不用转了。
x 是目标节点的子节点。
那我们直接转一下 x 就可以了。
对于 x 的父亲也不是目标节点的情况,我们也分两种情况讨论。
x 的父亲也不是目标节点,且 x 与其父亲的所在子树类型相同。
可以理解为 x,x 的父亲和 x 的父亲的父亲三个节点在一条直线上。
这样的话,我们就先旋转 x 的父节点,再旋转 x。
x 的父亲也不是目标节点,且 x 与其父亲的所在子树类型不同。
可以理解为 x,x 的父亲和 x 的父亲的父亲三个节点的连线是一条折线。
这样的话,我们旋转两次 x。
这样不断判断,直到 x 到达目标节点。
同时我们需要注意,因为我们根节点是随着我们的不断旋转而不断变化的,所以我们需要即使更新根节点的信息。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| void splay(int x, int k)
{
while(tr[x].fa != k)
{
int y = tr[x].fa, z = tr[y].fa;
if(z != k)
{
if((tr[y].s[1] == x) ^ (tr[z].s[1] == y))
rotate(x);
else
rotate(y);
}
rotate(x);
}
if(!k) rt = x;
}
|
其他操作
我们假设我们需要维护的是一棵可重序列的二叉搜索树。
插入
Splay 的插入操作是比较复杂的。
假设我们需要向树中插入一个元素 ,那么我们分下列几种情况讨论:
- 如果树是空的,那就直接插入根节点。
- 如果当前节点的权值等于 ,那就增加当前节点的大小,并更新其与其父亲的信息。
- 否则就按照二叉搜索树的性质继续向下面的节点查找。
最后不要忘记将节点旋转到根。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| void insert(int k)
{
if(!rt)
{
tr[++idx].init(k, 0);
rt = idx;
return;
}
int p = rt, fa = 0;
while(true)
{
if(tr[p].v == k)
{
tr[p].w++;
pushup(p), pushup(fa);
splay(p, 0);
break;
}
fa = p;
p = tr[p].s[tr[p].v < k];
if(!p)
{
tr[++idx].init(k, fa);
tr[fa].s[tr[fa].v < k] = idx;
pushup(fa);
splay(idx, 0);
break;
}
}
}
|
删除
Splay 不使用惰性删除,其删除操作也是比较复杂的。
假设我们想要删除节点 。
首先,我们将 旋转到根。
然后我们分类讨论:
- 如果 的大小不为 1,那就减少其大小。
- 否则直接合并其两棵子树。
合并两棵树的操作很简单。如果我们假设需要合并的两棵树 和 中, 的最大值大于 的话,只需要将的 的最大值旋转到根,同时将 设置为其根节点的右子树即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| void loschn(int k)
{
get_rk(k);
if(tr[rt].w > 1)
{
tr[rt].w--;
pushup(rt);
return;
}
if(!tr[rt].s[0] && !tr[rt].s[1])
{
tr[rt].clear();
rt = 0;
return;
}
if(!tr[rt].s[0])
{
int p = rt;
rt = tr[rt].s[1];
tr[rt].fa = 0;
tr[p].clear();
return;
}
if(!tr[rt].s[1])
{
int p = rt;
rt = tr[rt].s[0];
tr[rt].fa = 0;
tr[p].clear();
return;
}
int p = rt, x = precrs();
tr[tr[p].s[1]].fa = x;
tr[x].s[1] = tr[p].s[1];
tr[p].clear();
pushup(rt);
}
|
查询 k 的排名
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| int get_rk(int k)
{
int res = 0, p = rt;
while(true)
{
if(k < tr[p].v)
{
p = tr[p].s[0];
}
else
{
if(tr[p].s[0])res += tr[tr[p].s[0]].sz;
if(k == tr[p].v)
{
splay(p, 0);
return res + 1;
}
res += tr[p].w;
p = tr[p].s[1];
}
}
return -1;
}
|
查询排名为 k 的数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| int get_k(int k)
{
int p = rt;
while(true)
{
if(tr[tr[p].s[0]].sz >= k)
{
p = tr[p].s[0];
}
else
{
k -= tr[p].w;
if(tr[p].s[0])k -= tr[tr[p].s[0]].sz;
if(k <= 0)
{
splay(p, 0);
return tr[p].v;
}
p = tr[p].s[1];
}
}
return -1;
}
|
查询 k 的前驱或后继
前驱定义为小于这个数的最大数,后继定义为大于这个数的最小数。
我们的思路是,先将其插入进去,这样它就会到根节点;然后查询其左子树内的最大值或右子树内的最小值即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int precsr()
{
int p = tr[rt].s[0];
if(!p)return p;
while(tr[p].s[1])p = tr[p].s[1];
splay(p, 0);
return p;
}
int succsr()
{
int p = tr[rt].s[1];
if(!p)return p;
while(tr[p].s[0])p = tr[p].s[0];
splay(p, 0);
return p;
}
|
例题
维护可重有序序列
洛谷板子题,要求我们支持维护一个有序序列,并支持上面讲的六种操作。
示例代码:Luogu P3369-splay
维护不可重序列,支持区间翻转
给个洛谷板子题的代码:
它这里面要求区间翻转,那么我们在进行每一次旋转操作时,我们首先将左边界的前驱旋转至根节点,接着再把右边界的后继旋转至根节点的下面,此时右边界的后继的左子树就是我们所要翻转的区间了。
我们顺便增加一个 flag 标记,用来标记翻转次数。
示例代码:Luogu P3391




来做第一个留言的人吧!