KMP 算法与前缀函数

发表于 更新于 分类于 本文字数： 1809 阅读时长 ≈ 5 分钟

KMP算法与前缀函数。

简介

KMP算法，全称为 Knuth-Morris-Pratt 算法，是由 Knuth, Morris 和 Pratt 这三个人创造的算法，可以在 $O(n+m)$ 的时间内使用 $O(n)$ 的空间完成如下的任务：

给定一个字符串 $S$ 和一个模式串 $T$，求出 $S$ 在 $T$ 中所有出现的位置。

其中 $|S| = n$，$|T| = m$。

KMP算法主要依赖的是 “Next函数” 这个东西。

Next函数

Next函数，有时候也被称作 “前缀函数”，是KMP算法的核心部分。
我们以一个数组 $\pi$ 来表示它。

其旨在求得任意一个前缀的border长度。

什么是border？

border指的是一个字符串内，真前缀和真后缀相等的那一部分。
这样的真前缀和真后缀可能有很多种，我们需要找的是最长的那一组。

真前缀和真后缀说的是前缀和后缀中除去字符串本身之后剩下的部分。

如何求得border？

朴素算法

我们显然可以暴力扫，最终的复杂度是 $O(n^3)$ 的。

懒得写了，直接搬了OI-Wiki的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// C++ Version
vector<int> prefix_function(string s)
{
    int n = ( int )s.length();
    vector<int> pi(n);
    for(int i = 1; i < n; i++)
        for(int j = i; j >= 0; j--)
            if(s.substr(0, j) == s.substr(i - j + 1, j))
            {
                pi[i] = j;
                break;
            }
    return pi;
}
1
2
3
4
5
6
7
8
9
10
# Python Version
def prefix_function(s):
    n = len(s)
    pi = [0] * n
    for i in range(1, n):
        for j in range(i, -1, -1):
            if s[0 : j] == s[i - j + 1 : i + 1]:
                pi[i] = j
                break
    return pi

优化

我们会发现，相邻的两个函数值最多会增加1。

也就是说，当我们移动到下一个位置时，Next函数的值要么增加一，要么维持不变，要么减少。

此时改进的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// C++ Version
vector<int> prefix_function(string s)
{
    int n = ( int )s.length();
    vector<int> pi(n);
    for(int i = 1; i < n; i++)
        for(int j = pi[i - 1] + 1; j >= 0; j--)  // improved: j=i => j=pi[i-1]+1
            if(s.substr(0, j) == s.substr(i - j + 1, j))
            {
                pi[i] = j;
                break;
            }
    return pi;
}
1
2
3
4
5
6
7
8
9
10
# Python Version
def prefix_function(s):
    n = len(s)
    pi = [0] * n
    for i in range(1, n):
        for j in range(pi[i - 1] + 1, -1, -1):
            if s[0 : j] == s[i - j + 1 : i + 1]:
                pi[i] = j
                break
    return pi

此时，我们每一个前缀最多需要比对 $O(n)$ 级别的字符串，总复杂度降到了 $O(n^2)$。

继续优化

刚才我们只考虑到了 $s[i+1] = s[\pi[i]]$ 的情况，即函数值增加1。
那么对于其他的情况呢？

我们考虑 $s[i+1] \neq s[\pi[i]]$。
在我们之前的想法里面，我们就需要枚举出来可能的border长度，并与实际情况进行比较。

我们尝试避免这些无谓的比较。

我们尝试找到一个前缀，在保证其与后缀相等的前提下，使得我们当前匹配的进度最大地保留下来。

观察一下我们想要找到的东西：

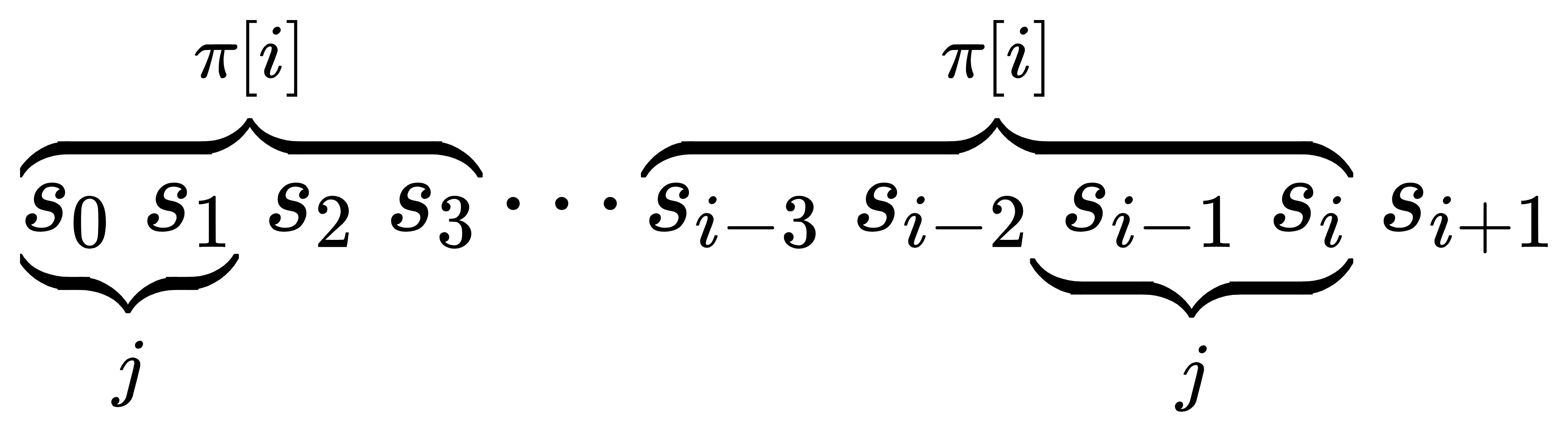
我们想要找到两个字符串 $s[0 \to j-1]$ 和 $s[i-j+1 \to i]$，他们完全相等，同时也分别是 $s[0 \to i]$ 的一个前缀和一个后缀。

我们发现，这两个字符串是完全包含在 $s[0 \to \pi[i]-1]$ 和 $s[i-\pi[i]+1 \to i]$ 这两个完全相等的字符串内的。

所以，我们就可以将其转化成为寻找字符串 $s[0 \to \pi[i]-1]$ 的border。

所以说，我们需要找的就是 $s[0 \to \pi[\pi[i]]-1]$ 和 $s[i-\pi[\pi[i]]+1 \to i]$。

然后我们尝试将 $s_{i+1}$ 纳入我们当前找到的border里面。

如果匹配，那就向前移动；
如果失配，那就继续寻找当前长度的border，直到最后到达0。

此时改进的算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// C++ Version
vector<int> prefix_function(string s)
{
    int n = ( int )s.length();
    vector<int> pi(n);
    for(int i = 1; i < n; i++)
    {
        int j = pi[i - 1];
        while(j > 0 && s[i] != s[j]) j = pi[j - 1];
        if(s[i] == s[j]) j++;
        pi[i] = j;
    }
    return pi;
}
1
2
3
4
5
6
7
8
9
10
11
12
# Python Version
def prefix_function(s):
    n = len(s)
    pi = [0] * n
    for i in range(1, n):
        j = pi[i - 1]
        while j > 0 and s[i] != s[j]:
            j = pi[j - 1]
        if s[i] == s[j]:
            j += 1
        pi[i] = j
    return pi

同时我们还可以发现，我们进行优化过的算法是一个在线算法。

KMP

现在终于来到了KMP算法的本体部分。

我们考虑根据题目给定的 $S$ 和 $T$ 两个字符串，拼接成一个新的字符串 $S+ \# +T$ ，其中 $\#$ 代表在 $S$ 和 $T$ 中都没有出现过的分隔符。

我们考虑计算新字符串 $T$ 部分的Next函数。

因为对于 $T$ 部分的每一个位置，其位置所对应的前缀绝对包含 $S$ 和分隔符的。
所以，其Next函数长度绝对不会超过 $n$。（即 $|S|$）

同时，我们保证了只会比对 $T$ 部分的字串，因为分隔符的出现使得包含其的后缀无法与同样长度的前缀匹配，因为这个字符不在 $S$ 或 $T$ 中出现过，而假如前缀中也包含了它，也会因为位置不一样而无法匹配。

所以说，如果在某一个位置 $i$ 有 $\pi[i] = n$ 成立，那么 $S$ 就会在 $T$ 的 $i-2n$ 处出现。

洛谷例题：https://www.luogu.com.cn/problem/P3375

示例代码：Luogu P3375

应用

求一个字符串的周期

我们考虑利用border的性质。

如果一个字符串 $s$ 有长度为 $r$ 的border，那么 $|s| - r$ 一定是 $s$ 的周期，其长度我们这里记作 $p$。

就像这样：

kmp2.svg

从这里我们可以得出 $s[0 \to 1]=s[2 \to 3]=s[4 \to 5]=s[6 \to 7]$，从而得出 $r-|s|=2$ 为 $s$ 的周期。

同时，如果这个周期的长度 $p$ 可以被 $|s|$ 整除的话，那么长度为 $p$ 的前缀就是 $s$ 的最小循环元。

AcWing例题：https://www.acwing.com/problem/content/143/

参考代码：AcWing 141