2-SAT 问题
一种奇怪的问题。
2-SAT问题的名字可以拆成两部分:2和SAT。
SAT?
SAT是Satisfiability【可满足性】的简称。
解释一下,就是,我们有若干个需要赋值的布尔变量,要求对这些变量进行赋值,使得这些变量的值满足一组布尔方程。
举个例子:
宝硕需要讲解一个题目,他需要就着代码讲题,所以代码需要让每一个人看懂,并尽量满足每一个人的代码习惯。
听的人有三个:KaiserWilheim、Johnsonloy、JeffZhao。现在他们提出了一些要求,如下:
- KaiserWilheim要求代码满足下列条件之一:
- 使用bits库 ($a$)
- 不使用
#define int long long($\neg b$) - 大括号换行 ($c$)
- Johnsonloy要求代码满足下列条件之一:
- 使用bits库 ($a$)
- 使用
#define int long long($b$) - 大括号换行 ($c$)
- JeffZhao要求代码满足下列条件之一:
- 不使用bits库 ($\neg a$)
- 不使用
#define int long long($\neg b$) - 大括号不换行 ($\neg c$)
我们可以将三种条件分别设为 $a$,$b$,$c$,变量前加 $\neg$ 表示对当前要求表示否定。
那么上述要求可以变为 $(a \lor \neg b \lor c)\land(a \lor b \lor c)\land(\neg a \lor \neg b \lor \neg c)$。其中 $\lor$ 表示或,$\land$ 表示与。
现在我们需要为 $abc$ 三个变量赋值,满足三个人的要求。
怎么处理呢?
暴力。
因为SAT问题已经被证明为了NPC(NP完全)问题,只能暴力做。
2-SAT?
那么2-SAT又是一种什么东西?
为什么我们需要把2-SAT单独拎出来?
2-SAT,就是每一个同学只有两个条件。
上面的问题就可以叫做3-SAT。
假如说Wilheim和Johnson一致决定将Jeff放在火刑架上使得Jeff放弃了大括号不换行,那么我们的问题就剩下了两个,要求就变为了 $(a \lor \neg b)\land(a \lor b)\land(\neg a \lor \neg b)$。
然后,宝硕就决定按照使用bits库和不使用#define int long long来作为讲题用的代码风格。
求解
我们怎么求解2-SAT问题呢?
使用强连通分量。
我们将每一个变量拆成两个点,记为 $x$ 与 $\neg x$。
对于每一个同学的要求 $(a \lor b)$,我们尝试将其转化为 $\neg a \to b \land \neg b \to a$。
因为我们需要使 $a$ 和 $b$ 中间至少有一个是真,那么我们一旦 $a$ 为假那么 $b$ 就一定为真,反之同理。
那么我们这样建图:
| 式子 | 建图 |
|---|---|
| $a \lor b$ | $\neg a \to b \land \neg b \to a$ |
| $\neg a \lor b$ | $a \to b \land \neg b \to \neg a$ |
| $a \lor \neg b$ | $\neg a \to \neg b \land b \to a$ |
| $\neg a \lor \neg b$ | $a \to \neg b \land b \to \neg a$ |
上面的图就变成了这个样子:
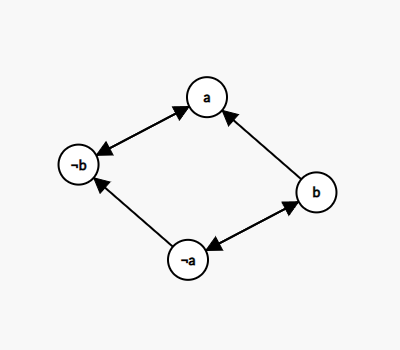
我们可以发现,$a$ 和 $\neg b$ 在同一强连通分量内,同时 $\neg a$ 和 $b$ 也在同一强连通分量内。
在同一强连通分量内就代表着知道了一个数的值之后就可以推出其他所有变量的值,所以我们给同一个强连通分量内的变量取值是相同的。
那么我们就给 $a$ 和 $\neg b$ 都取真,那么就意味着 $a=1,b=0$。
当然我们也可以给 $\neg a$ 和 $b$ 取真,也是一个可行解。
习惯上,我们给缩点后的图排一个拓扑序,当 $x$ 所在强连通分量的拓扑序在 $\neg x$ 所在的强连通分量的拓扑序之后的话我们就给 $x$ 取真。
那么我们什么时候才没有可行解呢?
当且仅当 $x$ 与 $\neg x$ 在同一个强连通分量里面的时候。
这样 $x$ 需要同时取真和假两个值,整个方程组就无解了。
实现
用tarjan来求强联通分量就可以了。
tarjan同时还给缩点后的图排了一下序,就不需要我们再排拓扑序了。
洛谷例题:https://www.luogu.com.cn/problem/P4782
1 |
|